��Ŀ����
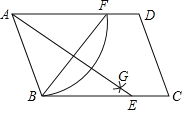
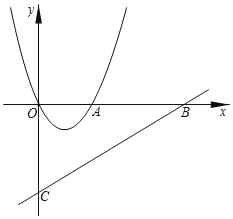
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�A��1��1������A���߶�AB��y�ᣨB��A�·�������ABΪ��������������ABCD�����B��������Ϊm�����κ���y��ax2��4ax��ͼ��Ķ���ΪE��
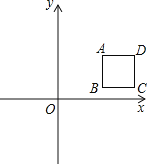
��1��AB���� �������ú�m�Ĵ���ʽ��ʾ����
��2������Aǡ���ڶ��κ���y��ax2��4ax��ͼ����ʱ������κ���y��ax2��4ax�Ĺ�ϵʽ��
��3������EǡΪ�߶�BC���е�ʱ������D�ķ����������Ĺ�ϵʽ��
��4����a��m+1�������κ���y��ax2��4ax��ͼ��ǡ��������ABCD�����������Ҷ��κ�������E��λ��ֱ��BC�·�ʱ��ֱ��д��m��ֵ��
���𰸡���1��1��m����2��![]() ����3��
����3��![]() ����4��m��ֵΪ��
����4��m��ֵΪ��![]() ��
��![]() ��
��![]() ��
��
��������
��1����AB��y���֪��A��B��������ȣ���B��A�·������Ե�A�������ȥ��B�����꼴ΪAB�ij���
��2���ѵ�A���������κ�����ϵʽ���ⷽ�����a���ɣ�
��3�������������ı���ȿ���m��ʾ��B��C��D�����꣬������m��ʾBC�е�E�ĺ����ꣻ�Ѷ��κ�����ϵʽ�䷽���õ�����E�ĺ�����Ϊ2���еù���m�ķ��̣����m��ֵ����õ�D���꣬�����ô���ϵ������÷�����������ϵʽ��
��4����a��m+1�Ͷ��κ�������E��λ��ֱ��BC�·������������m��ȡֵ��Χ��a��ȡֵ��Χ��������ͼ���֣���a��0ʱ��ֻ�е�����E���߶�BC��ʱ������������ABCD���������㣬�����ʱm��a��ֵ�������x��1��x��2��mʱ�������ϵĵ�������꣬���������߶�AB��CD�ϣ����Գ�������a��0ʱ�����������������E���߶�AD�ϻ��A���������ϣ��ֱ����m��a��ֵ��ͨ������˵��������
�⣺��1����yA��1��yB��m��AB��y���ҵ�B�ڵ�A�·�
��AB��yA��yB��1��m
�ʴ�Ϊ��1��m��
��2���ߵ�A��1��1���ڶ��κ���y��ax2��4ax��ͼ����
��a��4a��1
��a��![]()
����κ����Ĺ�ϵʽy��![]() x2+
x2+![]() x
x
��3����y��ax2��4ax��a��x��2��2��4a
����κ���ͼ��E��2����4a��
��������ABCD��A��1��1����yB��m��AB��y��
��B��1��m����BC��CD��DA��AB��1��m
��C��2��m��m����D��2��m��1��
�ߵ�E��BC�е�
��xE��![]()
��![]() ��2
��2
��ã�m����1
��D��3��1��
�ྭ����D�ķ����������Ĺ�ϵʽΪy��![]()
��4���ߵ�E��2����4a����λ��ֱ��BC�·�
�ੁ4a��m
��a��m+1
�ੁ4��m+1����m
��ã�m��![]()
�ٵ�a��0ʱ�������߿������ϣ�ֻ�е�����E���߶�BC��ʱ������������ABCD���������㣨��ͼ1��
��m��![]() ��a��
��a��![]()
��y��![]() x2
x2![]() x��B��1��
x��B��1��![]() ����C��
����C��![]() ��
��![]() ��
��
��x��1ʱ��y��![]() ��x��
��x��![]() ʱ��y��
ʱ��y��![]() ��
��
�����������߶�AB��CD�н��㣬����������ABCD����3������
��m��![]() ����
����
�ڵ�a��0ʱ�������߿������£�xD��2��m��3�����Ե�A�ȵ�D�������߶Գ���ֱ��x��2��
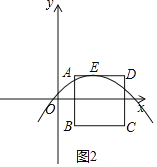
��ͼ2��������E���߶�AD�ϣ���a��![]() ��m��
��m��![]() ��
��
��y��![]() x2+x��A��1��1����D��
x2+x��A��1��1����D��![]() ��1��
��1��
��x��1ʱ��y��![]() +1��
+1��![]() ��1��x��
��1��x��![]() ʱ��y��
ʱ��y��![]() ��
��
�����������߶�AB��CD�н��㣬����������ABCD����3������
��m��![]() ����
����
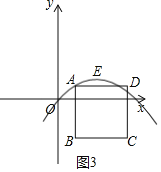
��ͼ3���������߹���A�����A���ڶԳ���ԳƵĵ������߶�AD��
����������������ABCD����3������
��a��![]() ��m��
��m��![]() ��
��
������������m��ֵΪ![]() ��
��![]() ��
��![]() ��
��


 Сѧ��ĩ���100��ϵ�д�
Сѧ��ĩ���100��ϵ�д� ��ĩ��ϰ���ϵ�д�
��ĩ��ϰ���ϵ�д� ����ѧ�䵥Ԫ������ĩר����100��ϵ�д�
����ѧ�䵥Ԫ������ĩר����100��ϵ�д� �Ƹ�360�ȶ����ܾ�ϵ�д�
�Ƹ�360�ȶ����ܾ�ϵ�д�����Ŀ��ȫ�����˶��ѳ�Ϊһ��ʱ�У�Ϊ���˽����о������˶��������ij�����ݵĹ�����Ա��չ��һ���ʾ����飬�ʾ����������Ŀ��A���������˶���B�����㳡����C���μӱ����ţ�D��ɢ����E�����˶���
�����Ǹ��ݵ��������Ƶ�ͳ��ͼ����һ���֣�
�˶���ʽ | A | B | C | D | E |
���� | 12 | 30 | m | 54 | 9 |
�������������Ϣ���ش��������⣺
��1�������ʾ�����Ĺ����� ���ˣ�ͼ���е�m=�� ����n=�� ����
��2��ͳ��ͼ�У�A������Ӧ������Բ�ĽǵĶ���Ϊ�� ����
��3�����ݵ�����������������ϲ�����˶���ʽ���� �������˶���������ռ�İٷֱ����� ����
��4�����б�ɳ�ڹ��Ǹ�������ϲ�����˶�����֮һ��ÿ������������������������ڽ���ij����Լ��1500�ˣ���ô����һ�¸������μӱ�ɳ�������������Ĵ�Լ�ж����ˣ�