Question

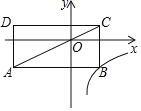
【题目】如图，在平面直角坐标系中，矩形ABCD的对角线AC经过坐标原点O，矩形的边分别平行于坐标轴，点B在函数（k≠0，x＞0）的图象上，点D的坐标为（﹣4，1），则k的值为（　　）

A.B.C.4D.﹣4

Answer 1

【答案】D

【解析】

由于点B的坐标不能求出，但根据反比例函数的几何意义只要求出矩形OEBF的面积也可，依据矩形的性质发现S矩形OGDH＝S矩形OEBF，而S矩形OGDH可通过点D（﹣4，1）转化为线段长而求得．，在根据反比例函数的所在的象限，确定k的值即可．

解：如图，根据矩形的性质可得：S矩形OGDH＝S矩形OEBF，

∵D（﹣4，1），

∴OH＝4，OG＝1，

∴S矩形OGDH＝OHOG＝4，

设B（a，b），则OE＝a，OF＝﹣b，

∴S矩形OEBF，＝OEOF＝﹣ab＝4，

又∵B（a，b）在函数（k≠0，x＞0）的图象上，

∴k＝ab＝﹣4

故选：D．