Question

【题目】如图，在△ABC中，AB=AC，AB的垂直平分线交AB于N，交BC的延长线于M，∠A=40°.

⑴求∠NMB的大小；

⑵若将图中的∠A的度数改为70°，其余条件不变，则∠NMB= ；

⑶你发现有什么样的规律？若将∠A改为钝角，对这个问题规律性的认识是否需要加以修改？

Answer 1

【答案】（1）20°；（2）35°；（3）规律为：在等腰△ABC中，当AB=AC，∠A是锐角时，∠NMB的度数恰好为顶角∠A度数的一半；当∠A为钝角时，上述规律依然成立，不需要修改.

【解析】

（1）在等腰三角形ABC中可求出∠B，然后在△BMN中根据内角和求解;

（2）解法同（1）；

（3）依照（1）（2）的解法，找出∠NMB与∠A的关系，当∠A为钝角时，作出图形，根据三角形内角和定理进行证明.

解：（1）∵AB=AC

∴∠B=∠ACB

∴

∵MN⊥AB，

∴∠MNB=90°，

∴∠NMB=90°-∠B=90°-70°=20°

（2）当∠A=70°时，如下图所示，

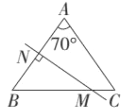
∵AB=AC

∴∠B=∠ACB

∴

∵MN⊥AB，

∴∠MNB=90°，

∴∠NMB=90°-∠B=90°-55°=35°

（3）如图，规律为：在等腰△ABC中，当AB=AC，∠A是锐角时，∠NMB的度数恰好为顶角∠A度数的一半，即∠NMB=∠A.

证明： ∵AB=AC

∴∠B=∠ACB

∴

∵MN⊥AB，

∴∠MNB=90°，

∴

即∠NMB的大小等于顶角∠A的一半.

当∠A为钝角时，上述规律依然成立，故不需要修改. 完整地叙述上述规律为：等腰三角形一腰上的垂直平分线与底边或底边的延长线相交，所成的锐角等于顶角的一半.

证明：如图，

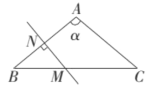
∵AB=AC

∴∠B=∠ACB

∴

∵MN⊥AB，

∴∠MNB=90°，

∴