��Ŀ����
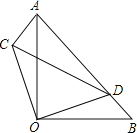
����Ŀ����ͼ����������ʻ�ڱ�ֱ�Ĺ�·�ϣ�����·����A��B��C��D�ĸ�վ�㣬ÿ������վ֮��ľ���Ϊ5ǧ�ף���Aվ����Dվ�ij���Ϊ���г�����Dվ����Aվ�ij���Ϊ���г�����һ�����г������г��ֱ��Aվ��Dվͬʱ������������У����Ժ����г������г�ÿ��10���ӷֱ���A��Dվͬʱ��һ����˿�ֻ�ܵ�վ���ϡ��³����ϡ��³���ʱ����Բ��ƣ������г������г����ٶȾ�Ϊ30ǧ��/Сʱ��
![]()
��1���ʵ�һ�����г���Bվ����һ�����г���Cվ�ֱ���ʱ���٣�
��2������һ�����г���ʻʱ��ΪtСʱ����һ�����г����һ�����г�֮��ľ���Ϊsǧ�ף���s��t�ĺ�����ϵʽ��
��3��һ�˿�ǰ��Aվ���£�����B��C��վ���P��������B��Cվ�����պ��������г���BP=xǧ�ף���ʱ���ӵ�֪ͨ��������35�����ڸϵ�������ѡ���ߵ�Bվ���ߵ�Cվ�����г�ǰ��Aվ�����˿͵IJ����ٶ���5ǧ��/Сʱ����x�����������
���𰸡���1��![]() ��
��![]() ����2����0��t��
����2����0��t��![]() ʱ��s=15��60t����
ʱ��s=15��60t����![]() ��t��
��t��![]() ʱ��s=60t��15����3��0��x��
ʱ��s=60t��15����3��0��x��![]() ��4��x��5��
��4��x��5��
��������
��1������ʱ��=·�̡��ٶ���ʽ������⣻
��2������t=![]() ʱ����һ�����г����һ�����г����������Է�0��t��
ʱ����һ�����г����һ�����г����������Է�0��t��![]() ��
��![]() ��t��
��t��![]() ����������ۼ��ɣ�
����������ۼ��ɣ�
��3���ɣ�2����֪ͬʱ������һ���ϡ����г���λ�ù���BC�е�Գƣ���˿͵���Aվ��ʱ��Ϊt���ӣ�����������������ۣ���x=2.5����x��2.5����x��2.5��
��1����һ�����г���Bվ��ʱ![]()
![]() Сʱ��
Сʱ��
��һ�����г���Cվ�ֱ���ʱ![]() Сʱ��
Сʱ��
��2����0��t��![]() ʱ��s=15��60t����
ʱ��s=15��60t����![]() ��t��
��t��![]() ʱ��s=60t��15��
ʱ��s=60t��15��
��3���ɣ�2����֪ͬʱ������һ���ϡ����г���λ�ù���BC�е�Գƣ���˿͵���Aվ��ʱ��Ϊt���ӣ�
�ٵ�x=2.5ʱ����Bվ��ʱ30���ӣ�����Ҫ�ٵ����г�5���ӣ�
t=30+5+10=45���������⣻
�ڵ�x��2.5ʱ��ֻ����Bվ�����г�������Bվxǧ�ף��������ұ���������г���CվҲ��xǧ�ף��������г���Bվ��5��x��ǧ�ף�
����ܳ����Ҳ�ĵ�һ�����г�����![]() ����ã�x��
����ã�x��![]() ��
��
��0��x��![]() ��
��
��18![]() ��t��20��
��t��20��
��0��x��![]() �������⣻
�������⣻
����˲����Ҳ��һ�����г���ֻ�ܳ��Ҳ�ڶ������г���x��![]() ��
��
![]() ����ã�x��
����ã�x��![]() ��
��
��![]() ��22
��22![]() ��t��28
��t��28![]() ��
��
��![]() �������⣻
�������⣻
����˲����Ҳ�ڶ������г���ֻ�ܳ��Ҳ���������г���x��![]() ��
��
![]() ����ã�x��
����ã�x��![]() ��
��
��![]() ��x��
��x��![]() ��35
��35![]() ��t��37
��t��37![]() ���������⣬
���������⣬
�����ϣ���0��x��![]() ��
��
�۵�x��2.5ʱ���˿�����Cվ�������г������������������г���Bվ�ǣ�5��x��ǧ�ף������ұ���������г���CվҲ�ǣ�5��x��ǧ�ף�
��������Ҳ��һ�����г�����![]() ����ã�x��5���������⣮
����ã�x��5���������⣮
��x��5���������⣮
����˲����Ҳ��һ�����г���ֻ�ܳ��Ҳ�ڶ������г���x��5��
![]() �����x��4��
�����x��4��
��4��x��5��30��t��32��
��4��x��5�������⣮
����˲����Ҳ�ڶ������г���ֻ�ܳ��Ҳ���������г���x��4��
![]() �����x��3��
�����x��3��
��3��x��4��42��t��44��
��3��x��4�������⣮
���ϣ���4��x��5��
����������0��x��![]() ��4��x��5��
��4��x��5��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˸�����������ˮ�ʣ�����������ij�����۹�˾��������10̨��ˮ�����豸������A��B�����ͺŵ��豸������ÿ̨�ļ۸��´�����ˮ�������
A�� | B�� | |
�۸���Ԫ/̨�� | a | b |
������ˮ������/�£� | 220 | 180 |
�����飺����һ̨A���豸�ȹ���һ̨B���豸��3��Ԫ������2̨A���豸�ȹ���3̨B���豸��3��Ԫ��
��1����a��b��ֵ��
��2����Ԥ�㣺�����۹�˾������ˮ�����豸���ʽ���100��Ԫ������Ϊ�ù�˾���ļ��ֹ�����
��3���ڣ�2���ʵ������£���ÿ��Ҫ��������ˮ��������1880�֣�Ϊ�˽�Լ�ʽ�����Ϊ���۹�˾���һ����ʡǮ�Ĺ�����