Question

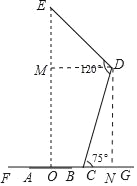
【题目】如图是在写字台上放置一本摊开的数学书和一个折叠式台灯时的截面示意图，已知摊开的数学书AB长20cm，台灯上半节DE长40cm，下半节DC长50cm．当台灯灯泡E恰好在数学书AB的中点O的正上方时，台灯上、下半节的夹角即∠EDC=120°，下半节DC与写字台FG的夹角即∠DCG=75°，求BC的长．（书的厚度和台灯底座的宽度、高度都忽略不计，F、A、O、B、C、G在同一条直线上．参考数据：sin75°≈0.97，cos75°≈0.26，≈1.41，结果精确到0.1）

Answer 1

【答案】BC= 5.2cm．

【解析】

如图，作DM⊥OE于M，DN⊥FG于N．则四边形DMON是矩形．根据题意求得∠EDM=45°，即可求得EM=DM=ON=20cm，在Rt△DCN中，求得CN的长，根据BC=ON﹣OB﹣CN即可求BC得长.

如图，作DM⊥OE于M，DN⊥FG于N．则四边形DMON是矩形．

∴DM∥ON，

∴∠DCN=∠CDM=75°，

∴∠EDM=120°﹣75°=45°，

∵DE=40cm，

∴EM=DM=ON=20≈28.2（cm），

在Rt△DCN中，CN=CDcos75°≈13（cm），

∵OB=10，

∴BC=ON﹣OB﹣CN=28.2﹣10﹣13=5.2（cm）．