题目内容
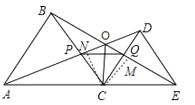
【题目】已知:如图,△ABC是等边三角形,延长AC到E,C为线段AE上的一动点(不与点A、E重合),在AE同侧分别作正三角形ABC和正三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC. 以下五个结论:①AD=BE;②AP=BO;③PQ//AE;④∠AOB=60°;⑤OC平分∠AOE;结论正确的有_________(把你认为正确的序号都填上)

【答案】①③④⑤
【解析】
根据等边三角形的三边都相等,三个角都是60°,可以证明△ACD![]() △BCE,根据全等三角形对应边相等可得AD=BE,所以①正确;
△BCE,根据全等三角形对应边相等可得AD=BE,所以①正确;
由△ACD![]() △BCE得∠CAD=∠CBE,加上∠BCA=∠DCE=60°,AC=BC,得到△ACP
△BCE得∠CAD=∠CBE,加上∠BCA=∠DCE=60°,AC=BC,得到△ACP![]() △BCQ(ASA),所以AP=BO,故②错误;
△BCQ(ASA),所以AP=BO,故②错误;
根据△ACP![]() △BCQ,再根据PC=QC,推出△PCQ是等边三角形,又由∠ACB=∠CPQ,根据内错角相等,两直线平行,故③正确;
△BCQ,再根据PC=QC,推出△PCQ是等边三角形,又由∠ACB=∠CPQ,根据内错角相等,两直线平行,故③正确;
利用等边三角形的性质,BC//DE,再根据平行线的性质得到∠CBE=∠DEO,于是∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.故④正确;
根据三角形面积公式求出CN=CM,根据角平分线性质即可判断⑤.
①∵正三角形ABC和正三角形CDE,
∴BC=AC,DE=DC=CE,∠DEC=∠BCA=∠DCE=60°,
∴∠ACD=∠BCE,
在△ACD和△BCE中,
 ,
,
∴△ACD![]() △BCE(SAS),
△BCE(SAS),
∴AD=BE;故①正确.
②∵△ACD![]() △BCE(已证),
△BCE(已证),
∴∠CAD=∠CBE,
∵∠BCA=∠DCE=60°(已证),
∴![]() =60°,
=60°,
∴∠ACB=∠BCQ=60°,
在△ACP和△BCQ中,
 ,
,
∴△ACP![]() △BCQ(ASA),
△BCQ(ASA),
∴AP=BO,
故②错误.
③∵△ACP![]() △BCQ(已证),
△BCQ(已证),
∴PC=QC,
∴△PCQ是等边三角形.
∴∠CPQ=60°,
∴∠ACB=∠CPQ,
∴PQ//AE,
故③正确.
④∵∠ACB=∠DCE=60°,
∴∠BCD=60°,
在正三角形CDE中,
∠DEC =60°=∠BCD,
∴ BC//DE,
∴∠CBE=∠DEO,
∴∠AOB=∠DAC+∠BEC=∠BEC+∠DEO=∠DEC=60°.
故④正确.
⑤过C作![]() 于M,
于M,![]() 于N,
于N,
∵△ACD![]() △BCE,
△BCE,
∴![]() ,BE=AD,
,BE=AD,
∴![]()
∴CM=CN,
∴OC平分∠AOE,故⑤正确;
故答案为①③④⑤.

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案







