题目内容
【题目】如图,在平面直角坐标系中,已知点A(0,2),△AOB和△APQ都是等边三角形.
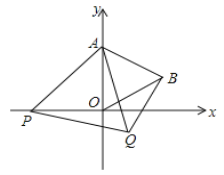

⑴求点B的坐标;
⑵试判断直线AB与直线BQ的位置关系,并证明;
⑶连接OQ,当OQ∥AB时,求P点的坐标.
【答案】(1)![]() ;(2)AB⊥BQ,证明见解析;(3)P
;(2)AB⊥BQ,证明见解析;(3)P![]() .
.
【解析】
(1)过B作BC⊥OC于点C,易得∠BOC=30°,借助直角三角形的边角关系即可解决问题;
(2)证明△APO≌△AQB,得到∠ABQ=∠AOP=90°,即AB⊥BQ;
(3)当点P在x轴负半轴上时,点Q在点B的下方,易得△BOQ为直角三角形,利用勾股定理求出BQ,由![]() 可知OP=BQ,从而得到P点坐标;当点P在x轴正半轴时,点Q必在第一象限,OQ和AB不可能平行.
可知OP=BQ,从而得到P点坐标;当点P在x轴正半轴时,点Q必在第一象限,OQ和AB不可能平行.
(1)如下图所示,过B作BC⊥OC于点C,
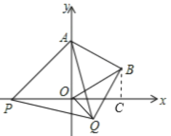
∵△AOB为等边三角形,且OA=2,
![]() ,
,![]()
![]() ,
,
![]()
![]() ,
,![]()
![]()
(2)AB⊥BQ,证明如下:
∵△APQ、△AOB都是等边三角形,
![]() ,
,![]() ,
,![]()
∴![]()
![]()
在△APO和△AQB中,
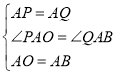
![]()
![]()
即AB⊥BQ.
(3)当点P在x轴负半轴上时,点Q在点B的下方,
![]() ∵AB∥OQ,AB⊥BQ,
∵AB∥OQ,AB⊥BQ,
∴OQ⊥BQ,∠BOQ=∠ABO=60°
∴∠BQO=90°
∴∠OBQ=30°,
在Rt△BOQ中,OB=OA=2,
∴![]() ,
,![]()
又∵![]()
![]()
∴此时P点坐标为![]()
当点P在x轴正半轴时,点Q必在第一象限,OQ和AB不可能平行.
所以当OQ∥AB时, P点的坐标为![]() .
.

练习册系列答案
相关题目







