Question

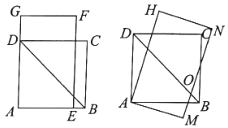
【题目】如图所示，四边形是边长为的正方形，长方形的宽，长．将长方形绕点顺时针旋转15°得到长方形（如图所示），这时与相交于点．则在图中，，两点间的距离是（ ）

A.B.5C.D.7

Answer 1

【答案】B

【解析】

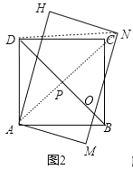
连接AN、DN，AN交BD于P点，如图2，根据旋转的性质得AM＝AE＝，MN＝EF＝，∠MAB＝15°，在Rt△AMN中，根据勾股定理计算出AN＝7，利用含30度的三角形三边的关系得到∠ANM＝30°，∠MAN＝60°，所以∠NAB＝∠NAM∠BAM＝45°，根据正方形的性质可得到点C在AN上，得到DP＝AP＝AB＝3，BD⊥AN，于是得到PN＝ANAP＝4，然后在Rt△PDN中，利用勾股定理计算DN．

连接AN、DN，AN交BD于P点，如图2，

∵长方形AEFG绕点A顺时针旋转15°得到长方形AMNH，

∴AM＝AE＝，MN＝EF＝，∠MAB＝15°，

在Rt△AMN中，∵AM＝，MN＝，

∴AN＝＝7，

∴∠ANM＝30°，∠MAN＝60°，

∴∠NAB＝∠NAM∠BAM＝45°，

∴点P为正方形ABCD的对角线的交点，即点C在AN上，

∴DP＝AP＝ABsin45°=AB＝×3＝3，BD⊥AN，

∴PN＝ANAP＝4，

在Rt△PDN中，DN＝＝5．

故选：B．