题目内容
【题目】探究:已知二次函数![]() 经过点
经过点![]() .
.
(1)求该函数的表达式;
(2)如图所示,点![]() 是抛物线上在第二象限内的一个动点,且点
是抛物线上在第二象限内的一个动点,且点![]() 的横坐标为
的横坐标为![]() ,连接
,连接![]() ,
,![]() ,
,![]() .
.
①求![]() 的面积
的面积![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求![]() 的面积的最大值,并求出此时点
的面积的最大值,并求出此时点![]() 的坐标.
的坐标.
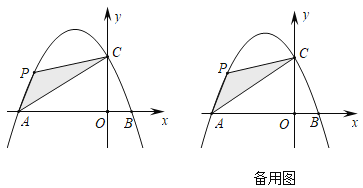
拓展:在平面直角坐标系中,点![]() 的坐标为
的坐标为![]() ,
,![]() 的坐标为
的坐标为![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个不同的交点,请直接写出
有两个不同的交点,请直接写出![]() 的取值范围.
的取值范围.
【答案】探究:(1)![]() ;(2)①
;(2)①![]()
![]() ,②
,②![]() 的面积的最大值是
的面积的最大值是![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ,拓展:
,拓展:![]() .
.
【解析】
(1)由待定系数法易求解析式;
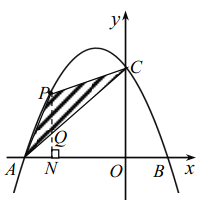
(2)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .设点
.设点![]() 的坐标为
的坐标为![]() ,由
,由![]() 可得关于t的二次函数,进而可求最大值.
可得关于t的二次函数,进而可求最大值.
(3)根据抛物线与MN的位置关系可知当抛物线经过M点时,a取最大值.
探究:(1)∵抛物线![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() .
.
∴抛物线的表达式为![]() .
.
(2)①过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() .
.
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() ,
,
![]() ,解得:
,解得:![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
∵点![]() 在抛物线
在抛物线![]() 上,点
上,点![]() 在直线
在直线![]() 上,
上,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,
,
∴![]()
![]() ,
,
∴![]()
![]() .
.
②∵![]() ,
,
∴当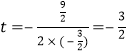 时,
时,![]() ,
,
当![]() 时,
时,![]() .
.
∴![]() 的面积的最大值是
的面积的最大值是![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() .
.
[拓展]:抛物线y=ax22x+3(a<0),当x=1时,y=a-2+3=a+1<3,故抛物线右边一定与MN有交点,
当x=-1,y=a+2+3=a+5,在M点或下方时,抛物线左边边一定与MN有交点,
即a+5≤3;
∴![]() ;
;

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】为弘扬中华传统文化,某校组织八年级1000名学生参加汉字听写大赛.为了解学生整体听写能力,赛后随机抽查了部分学生的成绩(得分取正整数,满分为100分)进行统计分析,并制作成图表:
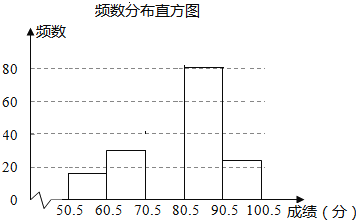
组别 | 分数段 | 频数 | 频率 |
一 | 50.5~60.5 | 16 | 0.08 |
二 | 60.5~70.5 | 30 | 0.15 |
三 | 70.5~80.5 | m | 0.25 |
四 | 80.5~90.5 | 80 | n |
五 | 90.5~100.5 | 24 | 0.12 |
请根据以上图表提供的信息,解答下列可题:
(1)这次随机抽查了______名学生,表中的数m=______,n=______;此样本中成绩的中位数落在第______组内;若绘制扇形统计图,则在修中“第三组”所对应扇形的圆心角的度数是______
(2)补全频数直方图;
(3)若成绩超过80分为优秀,请你估计该校八年级学生中汉字听写能力优秀的人数.