МвДҝДЪИЭ
ЎҫМвДҝЎҝТСЦӘ¶юҙОәҜКэy1=ax2+bx+cЈЁaЈҫ0Ј©өДНјПуУлxЦбҪ»УЪAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁnЈ¬0Ј©БҪөгЈ¬Т»ҙОәҜКэy2=2x+bөДНјПу№эөгAЈ®
ЈЁ1Ј©Ифa=![]() Ј®
Ј®
ўЩИф¶юҙОәҜКэy1=ax2+bx+cЈЁaЈҫ0Ј©УлyЦбҪ»УЪөгCЈ¬ЗуЎчABCөДГж»эЈ»
ўЪЙиy3=y1©Ғmy2Ј¬КЗ·сҙжФЪХэХыКэmЈ¬өұxЎЭ0КұЈ¬y3ЛжxөДФцҙу¶шФцҙуЈҝИфҙжФЪЈ¬ЗуіцХэХыКэmөДЦөЈ»ИфІ»ҙжФЪЈ¬ЗлЛөГчАнУЙЈ®
ЈЁ2Ј©Иф![]() ЈјaЈј
ЈјaЈј![]() Ј¬ЗуЦӨЈә©Ғ5ЈјnЈј©Ғ4Ј®
Ј¬ЗуЦӨЈә©Ғ5ЈјnЈј©Ғ4Ј®
Ўҫҙр°ёЎҝЈЁ1Ј©ўЩ![]() Ј»ўЪҙжФЪЈ¬m=1Ј»ЈЁ2Ј©јыҪвОц
Ј»ўЪҙжФЪЈ¬m=1Ј»ЈЁ2Ј©јыҪвОц
ЎҫҪвОцЎҝ
ЈЁ1Ј©ўЩҪ«өгAЧшұкҙъИлҪвОцКҪҝЙЗуb=2Ј¬c=2©ҒaЈ¬јҙҝЙЗуЕЧОпПЯҪвОцКҪЈ¬ҝЙЗуөгCЈ¬өгBЧшұкЈ¬УЙИэҪЗРОөДГж»э№«КҪҝЙЗуҪвЈ»
ўЪУЙy3=![]() x2+2x+
x2+2x+![]() ©ҒmЈЁ2x+2Ј©=
©ҒmЈЁ2x+2Ј©=![]() x2+ЈЁ2©Ғ2mЈ©x+ЈЁ
x2+ЈЁ2©Ғ2mЈ©x+ЈЁ![]() ©Ғ2mЈ©Ј¬УЙ¶юҙОәҜКэөДРФЦКҝЙЗуmЎЬ1Ј¬јҙҝЙЗуҪвЈ»
©Ғ2mЈ©Ј¬УЙ¶юҙОәҜКэөДРФЦКҝЙЗуmЎЬ1Ј¬јҙҝЙЗуҪвЈ»
ЈЁ2Ј©y1=ax2+2x+ЈЁ2©ҒaЈ©өД¶ФіЖЦбОӘx=©Ғ![]() =©Ғ
=©Ғ![]() Ј¬УЙ
Ј¬УЙ![]() ЈјaЈј
ЈјaЈј![]() Ј¬ҝЙөГ©Ғ3Јј©Ғ
Ј¬ҝЙөГ©Ғ3Јј©Ғ![]() Јј©Ғ
Јј©Ғ![]() Ј¬УЦAЈЁ©Ғ1Ј¬0Ј©ЎўBЈЁnЈ¬0Ј©БҪөг№ШУЪ¶ФіЖЦб¶ФіЖЈ¬Фт|©Ғ1©ҒЈЁ©Ғ
Ј¬УЦAЈЁ©Ғ1Ј¬0Ј©ЎўBЈЁnЈ¬0Ј©БҪөг№ШУЪ¶ФіЖЦб¶ФіЖЈ¬Фт|©Ғ1©ҒЈЁ©Ғ![]() Ј©|=|©Ғ
Ј©|=|©Ғ![]() ©Ғn|Ј¬јҙҝЙЗуҪвЈ®
©Ғn|Ј¬јҙҝЙЗуҪвЈ®
ҪвЈәЈЁ1Ј©ўЩЎЯy1=ax2+bx+cЈЁaЈҫ0Ј©№эөгAЈ¬
Ўаa©Ғb+c=0Ј¬
ЎЯy2=2x+bөДНјПу№эөгAЈ¬
Ўаb=2Ј¬
Ўаc=2©ҒaЈ»
ЎЯa=![]() Ј¬
Ј¬
Ўаc=2©Ғ![]() Ј¬
Ј¬
Ўаy1=![]() x2+2x+
x2+2x+![]() Ј¬
Ј¬
ЎЯ¶юҙОәҜКэy1=![]() x2+2x+
x2+2x+![]() УлyЦбҪ»УЪөгCЈ¬УлxЦбҪ»УЪAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁnЈ¬0Ј©БҪөгЈ¬
УлyЦбҪ»УЪөгCЈ¬УлxЦбҪ»УЪAЈЁ©Ғ1Ј¬0Ј©Ј¬BЈЁnЈ¬0Ј©БҪөгЈ¬
ЎаөгCЈЁ0Ј¬![]() Ј©Ј¬өгBЈЁ©Ғ3Ј¬0Ј©Ј¬
Ј©Ј¬өгBЈЁ©Ғ3Ј¬0Ј©Ј¬
ЎаAB=2Ј¬
ЎаЎчABCөДГж»э=![]() ЎБ2ЎБ
ЎБ2ЎБ![]() Ј»
Ј»
ўЪy3=![]() x2+2x+
x2+2x+![]() ©ҒmЈЁ2x+2Ј©=
©ҒmЈЁ2x+2Ј©=![]() x2+ЈЁ2©Ғ2mЈ©x+ЈЁ
x2+ЈЁ2©Ғ2mЈ©x+ЈЁ![]() ©Ғ2mЈ©Ј¬
©Ғ2mЈ©Ј¬
ЎЯФЪxЎЭ0КұЈ¬y3ЛжxөДФцҙу¶шФцҙуЈ¬
Ўа¶ФіЖЦбx=©Ғ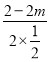 =2m©Ғ2ЎЬ0Ј¬
=2m©Ғ2ЎЬ0Ј¬
ЎаmЎЬ1Ј¬
ЎЯmКЗХэХыКэЈ¬
Ўаm=1Ј»
ЈЁ2Ј©ЎЯy1=ax2+2x+ЈЁ2©ҒaЈ©өД¶ФіЖЦбОӘx=©Ғ![]() =©Ғ
=©Ғ![]() Ј¬
Ј¬
УЦЎЯ![]() ЈјaЈј
ЈјaЈј![]() Ј¬
Ј¬
Ўа©Ғ3Јј©Ғ![]() Јј©Ғ
Јј©Ғ![]() Ј¬
Ј¬
УЦЎЯAЈЁ©Ғ1Ј¬0Ј©ЎўBЈЁnЈ¬0Ј©БҪөг№ШУЪ¶ФіЖЦб¶ФіЖЈ¬
Ўа|©Ғ1©ҒЈЁ©Ғ![]() Ј©|=|©Ғ
Ј©|=|©Ғ![]() ©Ғn|Ј¬
©Ғn|Ј¬
Ўаn=©Ғ![]() +1»тn=©Ғ1ЈЁЙбИҘЈ©Ј¬
+1»тn=©Ғ1ЈЁЙбИҘЈ©Ј¬
Ўа©Ғ5ЈјnЈј©Ғ4Ј®

 »ЖёФҙҙУЕҫнПөБРҙр°ё
»ЖёФҙҙУЕҫнПөБРҙр°ёЎҫМвДҝЎҝДі№Өі§ЙијЖБЛТ»ҝоіЙұҫОӘ20ФӘ/јюөД№ӨТХЖ·Н¶·ЕКРіЎҪшРРКФПъЈ¬ҫӯ№эөчІйЈ¬өГөҪИзПВКэҫЭЈә
ПъКЫөҘјЫ | Ўӯ | 30 | 40 | 50 | 60 | Ўӯ |
ГҝМмПъКЫБҝ | Ўӯ | 500 | 400 | 300 | 200 | Ўӯ |
ЈЁ1Ј©СРҫҝ·ўПЦЈ¬ГҝМмПъКЫБҝ![]() УлөҘјЫ
УлөҘјЫ![]() ВъЧгТ»ҙОәҜКэ№ШПөЈ¬Зуіц
ВъЧгТ»ҙОәҜКэ№ШПөЈ¬Зуіц![]() Ул
Ул![]() өД№ШПөКҪЈ»
өД№ШПөКҪЈ»
ЈЁ2Ј©өұөШОпјЫІҝГЕ№ж¶ЁЈ¬ёГ№ӨТХЖ·ПъКЫөҘјЫЧоёЯІ»ДЬі¬№э45ФӘ/јюЈ¬ДЗГҙПъКЫөҘјЫ¶ЁОӘ¶аЙЩКұЈ¬№ӨТХі§КФПъёГ№ӨТХЖ·ГҝМм»сөГөДАыИу8000ФӘЈҝ
ЎҫМвДҝЎҝЗлФД¶БТФПВІДБПЈ¬ІўНкіЙПаУҰИООсЈә
міІЁДЗЖхЈЁФј1170-1250Ј©КЗТвҙуАыКэС§јТЈ®1202ДкЈ¬Ч«РҙБЛЎ¶ЛгЕМКйЎ·Т»КйЈ¬ЛыКЗөЪТ»ёцСРҫҝБЛУЎ¶ИәН°ўАӯІ®КэС§АнВЫөДЕ·ЦЮИЛЈ¬Лы»№ФшФЪ°Јј°ЎўРрАыСЗЎўПЈА°Ј¬ТФј°ТвҙуАыОчОчАпәН·Ё№ъЖХВЮНъЛ№өИөШСРҫҝКэС§Ј®ЛыСРҫҝБЛТ»БР·ЗіЈЖжГоөДКэЈә0Ј¬1Ј¬1Ј¬2Ј¬3Ј¬5Ј¬8Ј¬13Ј¬21Ј¬34Ј¬55Ј¬89Ј¬144ЎӯЎӯХвБРКэЈ¬ұ»іЖОӘміІЁДЗЖхКэБРЈ®ЖдМШөгКЗҙУөЪ3ПоҝӘКјЈ¬ГҝТ»По¶јөИУЪЗ°БҪПоЦ®әНЈ¬міІЁДЗЖхКэБР»№УРәЬ¶аУРИӨөДРФЦКЈ¬ФЪКөјКЙъ»оЦРТІУР№г·әөДУҰУГЈ®

ИООсЈәЈЁ1Ј©МоРҙПВұнІўРҙіцНЁ№эМоұнДг·ўПЦөД№жВЙЈә
По | өЪ2По | өЪ3По | өЪ4По | өЪ5По | өЪ6По | өЪ7По | өЪ8По | өЪ9По | Ўӯ |
ХвТ»ПоөДЖҪ·Ҫ | 1 | 1 | 4 | 9 | 25 | ________ | _______ | 441 | Ўӯ |
ХвТ»ПоөДЗ°ЎўәуБҪПоөД»э | 0 | 2 | 3 | 10 | 24 | _______ | _______ | 442 | Ўӯ |
№жВЙЈә_____________Ј»
ЈЁ2Ј©ПЦУРіӨОӘ![]() өДМъЛҝЈ¬ТӘҪШіЙ
өДМъЛҝЈ¬ТӘҪШіЙ![]() РЎ¶ОЈ¬Гҝ¶ОөДіӨ¶ИІ»РЎУЪ
РЎ¶ОЈ¬Гҝ¶ОөДіӨ¶ИІ»РЎУЪ![]() Ј¬Из№ыЖдЦРИОТвИэРЎ¶О¶јІ»ДЬЖҙіЙИэҪЗРОЈ¬Фт
Ј¬Из№ыЖдЦРИОТвИэРЎ¶О¶јІ»ДЬЖҙіЙИэҪЗРОЈ¬Фт![]() өДЧоҙуЦөОӘ___________________Ј®
өДЧоҙуЦөОӘ___________________Ј®