题目内容
【题目】如图，在△ABC中，∠BAC=90°，∠B=45°，BC=10 cm，过点A作AD∥BC，且点D在点A的右侧．点P从点A出发沿射线AD方向以每秒1cm的速度运动，同时点Q从点C出发沿射线CB方向以每秒2cm的速度运动，在线段QC上取点E，使得QE =2cm，连结PE，设点P的运动时间为t秒．
（1）若PE⊥BC，则①PE= cm，CE= （用含t的式子表示）；
②求BQ的长；
（2）请问是否存在t的值，使以A，B，E，P为顶点的四边形为平行四边形？若存在，求出t的值；若不存在，请说明理由。
【答案】（1）①5，2t －2；②BQ=
；（2）存在t的值，使以A，B，E，P为顶点的四边形为平行四边形，t=4或12 s.
【解析】试题分析：（1）①作AM⊥BC于M，由已知条件得出AB=AC，由等腰三角形的性质得出BM=CM，由直角三角形斜边上的中线性质得出AM=
BC=5，从而得出PE的长，由CQ=2t，QE=2，得到CE的长；
②证出△APN和△CEN是等腰直角三角形，得出PN=AP=t，CE=NE=5﹣t，由CE=CQ﹣QE=2t﹣2得出方程，解方程即可；
（2）由平行四边形的判定得出AP=BE，得出方程，解方程即可．
试题解析：解：（1）①作AM⊥BC于M．∵∠BAC=90°，∠B=45°，∴∠C=45°=∠B，∴AB=AC，∴BM=CM，∴AM=
BC=5．∵PE⊥BC，∴PE=AM=5．∵AP=t，CQ=2t，∴CE=2t-2．
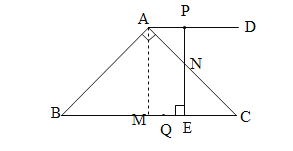
②由①可知：AM=
BC=5．∵AD∥BC，∴∠PAN=∠C=45°．∵PE⊥BC，∴PE=AM=5，PE⊥AD，∴△APN和△CEN是等腰直角三角形，∴PN=AP=t，CE=NE=5﹣t．∵CE=CQ﹣QE=2t﹣2，∴5﹣t=2t﹣2，解得：t=
，所以BQ=BC﹣CQ=10﹣2×
=
；
（2）存在，t=4；理由如下：
若以A，B，E，P为顶点的四边形为平行四边形，则AP=BE，∴t=10﹣2t+2或t=2t﹣2﹣10
解得：t=4或12，∴存在t的值，使以A，B，E，P为顶点的四边形为平行四边形，t=4或12．
