题目内容
【题目】四边形ABCD中,AB∥ DC , BC=b,AB=AC=AD=a,如图24-1-4-11,求BD的长.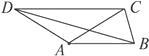
图24-1-4-11
【答案】解:∵AB=AC=AD=a,∴点B、C、D到A点距离相等.故以A为圆心,以a为半径作⊙A , 并延长BA交⊙A于E , 连结DE.
∵AB∥CD , ∴弧 BC=弧DE.∴BC=DE=b.
∵BE为⊙A的直径,∴∠EDB=90°.
在Rt△EDB中,BD= ![]() =
= ![]() ,∴BD的长为
,∴BD的长为 ![]() .
.
【解析】∵AB=AC=AD=a,∴点B、C、D到A点距离相等.故以A为圆心,以a为半径作⊙A,并延长BA交⊙A于E,连结DE.
∵AB∥CD,∴弧 BC=弧DE.∴BC=DE=b.
∵BE为⊙A的直径,∴∠EDB=90°.
在Rt△EDB中,BD= ![]() =
= ![]() ,∴BD的长为
,∴BD的长为 ![]() .
.
【考点精析】关于本题考查的勾股定理的概念和圆周角定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能得出正确答案.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目








