��Ŀ����
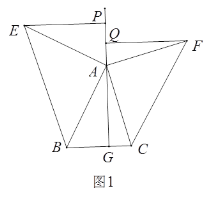
����Ŀ��̽������֪����ͼ1������ABC�У���ACB��90����AC��6��BC��8��D���߶�AB��һ�����㣮
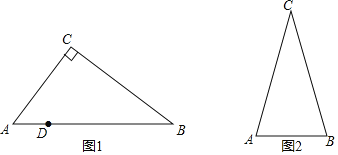
��1��������D����ֱ��AC��BC�ĶԳƵ�M��N��
��2���ڣ�1���������£�����MN
����֤��M��C��N������ͬһ��ֱ���ϣ�
����MN����Сֵ��
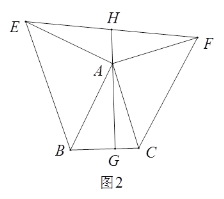
Ӧ�ã���֪����ͼ2������ABC�У���C��30����AC��CB��AB��3����ABC�����ΪS����D��E��F�ֱ���AB��AC��BC���������㣬���ú�S�Ĵ���ʽֱ�ӱ�ʾ��DEF���ܳ�����Сֵ������ͼ2�л������������ͼ�Σ�
���𰸡�̽������1������������2����֤������������MN����Сֵ��![]() ��Ӧ�ã���DEF���ܳ�����СֵΪ
��Ӧ�ã���DEF���ܳ�����СֵΪ![]() ���������������ͼ�μ�����.
���������������ͼ�μ�����.
��������
��1�����ݶԳƵ��������ͼ���ɣ�
��2�������öԳƵ����ʽ�ϡ�ACB��90��֤����MCN��180�㼴����
���������֪MN��2CD�����Ե�CD��ABʱ��CD��ֵ��С���������������⼴�ɣ�
Ӧ�ã���ͼ2�У���D��AB������һ�㣬����D����ֱ��AC�ĶԳƵ�D������D����ֱ��BC�ĶԳƵ�D��������D��D����AC��E����BC��F����CH��AB��H���ɡ�DEF���ܳ���DE+EF+DF��D��E+EF+FD����D��D����CD���Ƴ�CD��ֵ��Сʱ����DEF���ܳ���С���ɴ˼��ɽ������.
̽������1���⣺��ͼ1�У���M��N��Ϊ����

��2����֤��������CD��CM��CN��
�ɶԳƵ����ʿ�֪����ACD����ACM����BCD����BCN��
�ߡ�ACD+��BCD��90����
���MCD+��NCD��2����ACD+��BCD����180����
��M��C��N������ͬһ��ֱ���ϣ�
�ڽ⣺��CM��CD��CN��CD��
��MN��CM+CN��2CD��
�൱CD���ʱ��MN��ֵ��С��
��CD��ABʱ�����߶���̣�
��CD����Сֵ��![]() ��
��
��MN����Сֵ��![]() ��
��
Ӧ�ã��⣺��ͼ2�У���D��AB������һ�㣬����D����ֱ��AC�ĶԳƵ�D������D����ֱ��BC�ĶԳƵ�D��������D��D����AC��E����BC��F����CH��AB��H��

�ɶԳƵ����ʿ�֪��CD��CD����CD����ED��ED����FD��FD������ACD����ACD������BCD����BCD����
���D��CD����2��ACB��60����
���D��CD���ǵȱ������Σ�
��D��D����CD����CD��
�ߡ�DEF���ܳ���DE+EF+DF��D��E+EF+FD����D��D����CD��
��CD��ֵ��Сʱ����DEF���ܳ���С��
���Ե�CD��CH�غ�ʱ��CD��ֵ��С��
��![]() ABCH��S����
ABCH��S����![]() ��
��
��CH��![]() ��
��
���![]() ��
��