题目内容
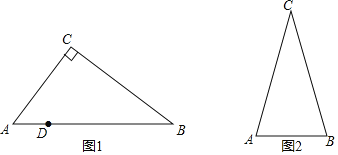
【题目】如图1，⊿ABC中，AG⊥BC于点G，以A为直角顶点，分别以AB、AC为直角边，向⊿ABC作等腰Rt⊿ABE和等腰Rt⊿ACF，过点E、F作射线GA的垂线，垂足分别为P、Q。
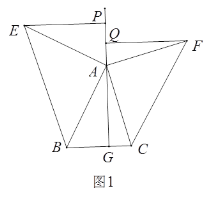
（1）求证：⊿AEP≌⊿BAG；
（2）试探究EP与FQ之间的数量关系，并证明你的结论；
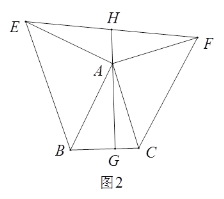
（3）如图2，若连接EF交GA的延长线于H，由（2）中的结论你能判断EH与FH的大小关系吗？并说明理由；
（4）在（3）的条件下，若BC=AG=10，请直接写出S⊿AEF= .
【答案】（1）答案见解析；（2）答案见解析；（3）答案见解析；（4）50.
【解析】
（1）根据等腰Rt△ABE的性质，求出∠EPA=∠EAB=∠AGB=90°，∠PEA=∠BAG，根据AAS推出△EPA≌△AGB；（2）根据全等三角形的性质推出EP=AG，同理可得△FQA≌△AGC，即可得出AG=FQ，最后等量代换即可得出答案；（3）求出∠EPH=∠FQH=90°，根据AAS推出△EPH≌△FQH，即可得出EH与FH的大小关系；（4）根据全等三角形△EPH≌△FQH，△EPA≌△AGB，△FQA≌△AGC，推出S△FQAS△AGC，S△FQH=S△EPH，S△EPA=S△AGB，即可求出S△AEF=S△ABC，根据三角形面积公式求出即可．
解：（1）如图1，∵∠EAB=90°，EP⊥AG，AG⊥BC，
∴∠EPA=∠EAB=∠AGB=90°，
∴∠PEA+∠EAP=90°，∠EAP+∠BAG=90°，
∴∠PEA=∠BAG，
在△EPA和△AGB中，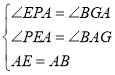
，
∴△EPA≌△AGB（AAS），
（2）EP=FQ，
证明：由（1）可得，△EPA≌△AGB，
∴EP=AG，
同理可得，△FQA≌△AGC，
∴AG=FQ，
∴EP=FQ；
（3）EH=FH，
理由：如图，∵EP⊥AG，FQ⊥AG，
∴∠EPH=∠FQH=90°，
在△EPH和△FQH中，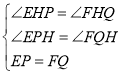
，
∴△EPH≌△FQH（AAS），
∴EH=FH．
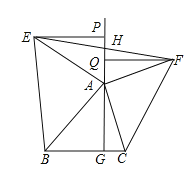
(4)∵△EPH≌△FQH，△EPA≌△AGB，△FQA≌△AGC，
∴S△FQA=S△AGC，S△FQH=S△EPH，S△EPA=S△AGB，
∴S△AEF=S△EPA+S△FQA=S△AGB+S△AGC=S△ABC=
×BC×AG=×10×10=50．
故答案为：50．
