题目内容
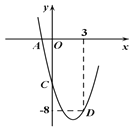
【题目】二次函数![]() 的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成
的部分图象如图所示,其中图象与x轴交于点A(-1,0),与y轴交于点C(0,-5),且经过点D(3,-8).(1)求此二次函数的解析式; (2)用配方法将将此二次函数的解析式写成![]() 的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
的形式,并直接写出此二次函数图象的顶点坐标以及它与x轴的另一个交点B的坐标.
【答案】(1)![]() ;(2)
;(2)![]() 顶点(2,-9) B(5, 0)
顶点(2,-9) B(5, 0)
【解析】
(1)把点A、B、C的坐标代入函数表达式,然后根据三元一次方程的解法求出a、b、c的值,即可得到二次函数的解析式;
(2)利用配方法整理,然后根据顶点式写出顶点坐标,再根据对称轴解析式与点A的坐标求出与x轴的另一交点坐标;
(1)根据题意得, ,
,
②分别代入①、③得,
a-b=5④,
3a+b=-1⑤,
④+⑤得,4a=4,
解得a=1,
把a=1代入④得,1-b=5,
解得b=-4,
∴方程组的解是 ,
,
∴此二次函数的解析式为y=x2-4x-5;
(2)y=x2-4x-5=x2-4x+4-4-5=(x-2)2-9,
二次函数的解析式为y=(x-2)2-9,
顶点坐标为(2,-9),
对称轴为x=2,
设另一点坐标为B(a,0),
则-1+a=2×2,
解得a=5,
∴点B的坐标是B(5,0).

 名校课堂系列答案
名校课堂系列答案【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.