题目内容
【题目】已知一次函数y=![]() x +m和y=-
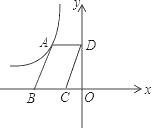
x +m和y=-![]() x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
x +n的图象都是经过点A(-2,0),且与y轴分别交于B、C两点.
(1)直接写出B、C两点的坐标B: ;C:
(2)求ABC的面积.
【答案】(1)(0,3),(0,-1),(2)4
【解析】
(1)题干要求直接写出B、C两点的坐标,令x=0分别代入求出y值即可.
(2)题干要求ABC的面积,根据(1)问B,C点坐标求出以BC为底边的边长从而求值.
解:(1)已知一次函数y=![]() x +m和y=-
x +m和y=-![]() x +n的图象都是经过点A(-2,0),将x=-2,y=0,分别代入有-3+m=0和1+n=0,求得m=3,n=-1,
x +n的图象都是经过点A(-2,0),将x=-2,y=0,分别代入有-3+m=0和1+n=0,求得m=3,n=-1,
又由与y轴分别交于B、C两点,可得B,C的横轴坐标为0即x=0,代入y=![]() x +m和y=-
x +m和y=-![]() x +n得到y=m和y=n,则y=3和y=-1,即B(0,3),C(0,-1).
x +n得到y=m和y=n,则y=3和y=-1,即B(0,3),C(0,-1).
(2)B,C都在y轴上,且B(0,3),C(0,-1),可求出BC=3-(-1)=4,
又A(-2,0)可知以BC为底边的高即为A点的横轴坐标的绝对值即2,则ABC的面积为![]()

【题目】观察下表:
序号 | 1 | 2 | 3 | … |
图形 | x x | |||
y | ||||
x x | x x x | |||
y y | ||||
x x x | ||||
y y | ||||
x x x | x x x x | |||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | ||||
y y y | ||||
x x x x | … |
我们把某格中字母的和所得到的多项式称为特征多项式,例如第1格的“特征多项式”为4x+y.回答下列问题:
(1)第2格的“特征多项式”为____,第n格的“特征多项式”为____;(n为正整数)
(2)若第1格的“特征多项式”的值为-8,第2格的“特征多项式”的值为-11.
①求x,y的值;
②在此条件下,第n格的“特征多项式”是否有最小值?若有,求最小值和相应的n值;若没有,请说明理由.