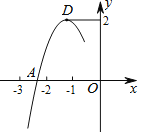Question

【题目】如图，在平面直角坐标系中，点A是抛物线与x轴正半轴的交点，点B在抛物线上，其横坐标为2，直线AB与y轴交于点点M、P在线段AC上不含端点，点Q在抛物线上，且MQ平行于x轴，PQ平行于y轴设点P横坐标为m．

（1）求直线AB所对应的函数表达式．

（2）用含m的代数式表示线段PQ的长．

（3）以PQ、QM为邻边作矩形PQMN，求矩形PQMN的周长为9时m的值．

Answer 1

【答案】（1）直线AB的解析式为；（2）见解析；（3）m的值为或．

【解析】试题分析：（1）先利用二次函数解析式求出A点和B点坐标，然后利用待定系数法求直线AB的解析式；

（2）设P（m，-m+8），则Q（m，-m2+4m），讨论：当0＜m≤2时，PQ=m2-5m+8；当2＜m＜8时，PQ=-m2+5m-8；

（3）先表示出M（m2-4m+8，-m2+4m），讨论：当0＜m≤2，QM=m2-5m+8，利用矩形周长列方程得到2（m2-5m+8+m2-5m+8）=9，然后解方程求出满足条件m的值；当2＜m＜8，QM=-m2+5m-8，利用矩形周长列方程得到2（-m2+5m-8-m2+5m-8）=9，然后解方程求出满足条件m的值．

试题解析：（1）当y=0时，-x2+4x=0，解得x1=0，x2=8，则A（8，0）；

当x=2时，y=-x2+4x=6，则B（2，6），

设直线AB所对应的函数表达式为y=kx+b，

将A（8，0），B（2，6）代入可得，

解得，

所以直线AB的解析式为y=-x+8；

（2）设P（m，-m+8），则Q（m，-m2+4m），

当0＜m≤2时，PQ=-m+8-（-m2+4m）=m2-5m+8；

当2＜m＜8时，PQ=-m2+4m-（-m+8）=-m2+5m-8；

（3）∵MQ∥x轴，

∴M点的纵坐标为-m2+4m，

∴M点的横坐标为m2-4m+8，即M（m2-4m+8，-m2+4m），

当0＜m≤2，QM=m2-4m+8-m=m2-5m+8，

∵2（PQ+QM）=9，

∴2（m2-5m+8+m2-5m+8）=9，

整理得2m2-20m+23=0，解得m1=，m2=（舍去）；

当2＜m＜8，QM=m-（m2-4m+8）=-m2+5m-8，

∵2（PQ+QM）=9，

∴2（-m2+5m-8-m2+5m-8）=9，

整理得2m2-20m+41=0，解得m1=，m2=（舍去）；

综上所述，m的值为或．