Question

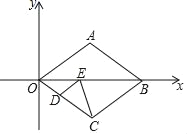
【题目】如图，在Rt△ABC中，已知∠C=90°，∠A=60°，AC=3cm，以斜边AB的中点P为旋转中心，把这个三角形按逆时针方向旋转90°得到Rt△A′B′C′，则旋转前后两个直角三角形重叠部分的面积为______________．

Answer 1

【答案】

【解析】

由点P是AB的中点，∠A=60°，AC=3cm可得BP的长，再由逆时针旋转90°，根据旋转的性质和30°直角三角形的三边比值，就可求出BM，MP的长，在Rt△B′MN和Rt△BNG中根据30°直角三角形的三边比值同样可以求出相应线段长，然后利用S阴影部分=进行计算即可．

如图，

∵∠C=90°，∠A=60°，AC=6，∴AB=2AC=6，∠B=30°，

∵点P为AB的中点，∴BP=3，

∵△ABC绕点P按逆时针方向旋转得到Rt△A′B′C′，

∴P=BP=3，

在Rt△BPM中，∠B=30°，∠BPM=90°，∴BM=2PM，∴PM=，BM=2，

∴B′M=B′P-PM=3-，

在Rt△B′MN中，∠B′=30°，∴MN=B′M=，∴BN=BM+MN=，

在Rt△BNG中，BG=2NG，BG2=NG2+BN2，∴NG=，

∴S阴影=S△BNG-S△BMP=，

故答案为：．