题目内容
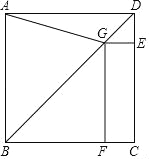
【题目】如图,在正方形ABCD中,点G在对角线BD上(不与点B,D重合),GE⊥DC于点E,GF⊥BC于点F,连结AG.
(1)写出线段AG,GE,GF长度之间的数量关系,并说明理由;
(2)若正方形ABCD的边长为1,∠AGF=105°,求线段BG的长.
【答案】(1)AG2=GE2+GF2(2)![]()
【解析】
试题分析:(1)结论:AG2=GE2+GF2.只要证明GA=GC,四边形EGFC是矩形,推出GE=CF,在Rt△GFC中,利用勾股定理即可证明;
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.易证AM=BM=2x,MN=![]() x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+
x,在Rt△ABN中,根据AB2=AN2+BN2,可得1=x2+(2x+![]() x)2,解得x=
x)2,解得x=![]() ,推出BN=
,推出BN=![]() ,再根据BG=BN÷cos30°即可解决问题.
,再根据BG=BN÷cos30°即可解决问题.
试题解析:(1)结论:AG2=GE2+GF2.
理由:连接CG.
∵四边形ABCD是正方形,
∴A、C关于对角线BD对称,
∵点G在BD上,
∴GA=GC,
∵GE⊥DC于点E,GF⊥BC于点F,
∴∠GEC=∠ECF=∠CFG=90°,
∴四边形EGFC是矩形,
∴CF=GE,
在Rt△GFC中,∵CG2=GF2+CF2,
∴AG2=GF2+GE2.
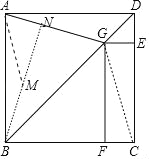
(2)作BN⊥AG于N,在BN上截取一点M,使得AM=BM.设AN=x.
∵∠AGF=105°,∠FBG=∠FGB=∠ABG=45°,
∴∠AGB=60°,∠GBN=30°,∠ABM=∠MAB=15°,
∴∠AMN=30°,
∴AM=BM=2x,MN=![]() x,
x,
在Rt△ABN中,∵AB2=AN2+BN2,
∴1=x2+(2x+![]() x)2,
x)2,
解得x=![]() ,
,
∴BN=![]() ,
,
∴BG=BN÷cos30°=![]() .
.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目



