题目内容
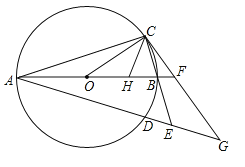
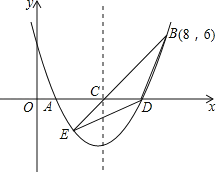
【题目】如图,二次函数y=![]() x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
x2+bx+c的图象交x轴于A、D两点并经过B点,已知A点坐标是(2,0),B点的坐标是(8,6).
(1)求二次函数的解析式;
(2)该二次函数的对称轴交x轴于C点,连接BC,并延长BC交抛物线于E点,连接BD,DE,求△BDE的面积;
(3)抛物线上有一个动点P,与A,D两点构成△ADP,是否存在2S△ADP=S△BCD?若存在请求出P点的坐标;若不存在,请说明理由.
【答案】(1)二次函数解析式为:y=![]() x2﹣4x+6;(2)
x2﹣4x+6;(2)![]() ;(3)存在,P1(4+
;(3)存在,P1(4+![]() ,
,![]() ),P2(4﹣
),P2(4﹣![]() ,
,![]() ),P3(3,﹣
),P3(3,﹣![]() ),P4(5,﹣
),P4(5,﹣![]() )
)
【解析】
(1)根据待定系数法可求二次函数的解析式;
(2)由题意可得C点,D点坐标,求出BC解析式,可求E点坐标,即可求△BDE的面积;
(3)点P到x轴的距离为h,根据2S△ADP=S△BCD,可求h=![]() ,再分点P在x轴上方,x轴下方讨论,可求点P坐标.
,再分点P在x轴上方,x轴下方讨论,可求点P坐标.
(1)∵二次函数y=![]() x2+bx+c的图象过A(2,0),B(8,6)
x2+bx+c的图象过A(2,0),B(8,6)
∴![]()
解得b=﹣4,c=6
∴二次函数解析式为:y=![]() x2﹣4x+6
x2﹣4x+6
(2)∵y=![]() x2﹣4x+6=y=
x2﹣4x+6=y=![]() (x﹣4)2﹣2,
(x﹣4)2﹣2,
∴函数图象的顶点坐标为(4,﹣2),
∴对称轴为直线x=4,点C坐标(4,0)
∵点A,点D是抛物线y=![]() x2﹣4x+6与x轴的交点
x2﹣4x+6与x轴的交点
∴点A,点D关于对称轴直线x=4对称,且A(2,0)
∴D(6,0)
设BC所在的直线解析式为y=kx+b,且过点B(8,6),点C(4,0)
∴![]()
解得k=![]() ,b=﹣6
,b=﹣6
∴BC所在的直线解析式为y=![]() x﹣6,
x﹣6,
∵E点是直线y=![]() x﹣6与抛物线y=
x﹣6与抛物线y=![]() x2﹣4x+6的交点,
x2﹣4x+6的交点,
∴![]() x﹣6=
x﹣6=![]() x2﹣4x+6
x2﹣4x+6
解得x1=3,x2=8(舍去),
当x=3时,y=﹣![]() ,
,
∴E(3,﹣![]() )
)
∴S△BDE=S△CDB+S△CDE=![]() ×2×6+
×2×6+![]() ×2×
×2×![]() =
=![]() .
.
(3)存在,
设点P到x轴的距离为h,
∵S△BCD=![]() ×2×6=6,S△ADP=
×2×6=6,S△ADP=![]() ×4×h=2h,且2S△ADP=S△BCD
×4×h=2h,且2S△ADP=S△BCD
∴2×2h=6,
解得h=![]() ,
,
当P在x轴上方时,
![]() =
=![]() x2﹣4x+6,解得x1=4+
x2﹣4x+6,解得x1=4+![]() ,x2=4﹣
,x2=4﹣![]() ,
,
当当P在x轴下方时,
﹣![]() =
=![]() x2﹣4x+6,
x2﹣4x+6,
解得x1=3,x2=5,
∴P1(4+![]() ,
,![]() ),P2(4﹣
),P2(4﹣![]() ,
,![]() ),P3(3,﹣
),P3(3,﹣![]() ),P4(5,﹣
),P4(5,﹣![]() )
)

【题目】今年,6月7日为端午节.在端午节前夕,三位同学到某超市调研一种进价为2元的粽子的销售情况.请根据小丽提供的信息,解答小华和小明提出的问题.
小丽 | 每个定价3元,每天能卖出500个.若这种粽子的售价每上涨0.1元,其销售量将减少10个 |
小华 | 照你说,若要实现每天800元的销售利润,那该如何定价?别忘了,根据物价局规定,售价不能超过进价的 |
小明 | 若按照物价局规定的最高售价,每天的利润会超过800元吗?请判断并说明理由 |