题目内容
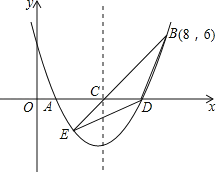
【题目】已知直线y=kx+2k+4与抛物线y=![]() x 2
x 2
(1)求证:直线与抛物线有两个不同的交点;
(2)设直线与抛物线分别交于A, B两点.
①当k=-![]() 时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
时,在直线AB下方的抛物线上求点P,使△ABP的面积等于5;
②在抛物线上是否存在定点D使∠ADB=90°,若存在,求点D到直线AB的最大距离. 若不存在,请你说明理由.
【答案】(1)见解析;①点P的坐标为(-2,2)或(1,![]() ),②存在,当CD⊥AB时,点D到直线AB的距离最大,最大距离为2
),②存在,当CD⊥AB时,点D到直线AB的距离最大,最大距离为2![]() .
.
【解析】
(1)联立y=kx+2k+4与y=![]() x 2,得到
x 2,得到![]() ,再利用根的判别式求解即可;(2) ①设P(m,
,再利用根的判别式求解即可;(2) ①设P(m,![]() m2),联立直线方程和抛物线方程,求得A,B的坐标,|AB|的长,运用点到直线的距离公式,解得即可得到所求P的坐标;②设A(x1,
m2),联立直线方程和抛物线方程,求得A,B的坐标,|AB|的长,运用点到直线的距离公式,解得即可得到所求P的坐标;②设A(x1,![]() x12),B(x2,
x12),B(x2,![]() x22),D(t,
x22),D(t,![]() t2),利用△ADE∽△DBF,得出AE·BF=DE·DF,再利用垂线段最短得出结果即可.
t2),利用△ADE∽△DBF,得出AE·BF=DE·DF,再利用垂线段最短得出结果即可.
(1)由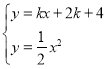 得
得![]()
∵![]()
=![]()
=![]()
=![]()
∵![]()
∴直线与抛物线有两个不同的交点.
(2)当k=-![]() 时,直线AB的解析式为y=-
时,直线AB的解析式为y=-![]() x+3
x+3
令-![]() x+3=
x+3=![]() x2,即x2+x-6=0,解得x1=-3,x2=2
x2,即x2+x-6=0,解得x1=-3,x2=2
∴点A的横坐标为-3,点B的横坐标为2
过点P作PQ∥y轴交直线AB于点Q
设P(m,![]() m2),则Q(m,-
m2),则Q(m,-![]() m+3)
m+3)
∴PQ=-![]() m+3-
m+3-![]() m2
m2
∵S△ABP=5,
∴![]() (2+3)(-
(2+3)(-![]() m+3-
m+3-![]() m2)=5
m2)=5
整理得:m2+m-2=0,解得m1=-2,m2=1
∴点P的坐标为(-2,2)或(1,![]() )
)
(3)设A(x1,![]() x12),B(x2,
x12),B(x2,![]() x22),D(t,
x22),D(t,![]() t2)
t2)
联立 消去y得:x2-2kx-4k-8=0
消去y得:x2-2kx-4k-8=0
∴x1+x2=2k,x1x2=-4k-8
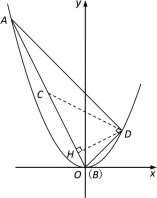
过点D作EF∥x轴,分别过点A、B作y轴的平行线,交EF于点E、F
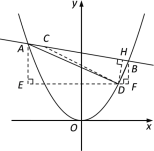
则DE=t-x1,AE=![]() x12-
x12-![]() t2,DF=x2-t,BF=
t2,DF=x2-t,BF=![]() x22-
x22-![]() t2
t2
由∠ADB=90°,可得△ADE∽△DBF
∴![]() ,即AE·BF=DE·DF
,即AE·BF=DE·DF
∴(![]() x12-
x12-![]() t2)(
t2)( ![]() x22-
x22-![]() t2)=(t-x1)(x2-t)
t2)=(t-x1)(x2-t)
∴t2+(x1+x2)t+x1x2+4=0
∴t2+2kt-4k-4=0,即2k(t-2)+t2-4=0
当t-2=0,即t=2时,上式对任意实数k均成立
即点D的坐标与k无关,∴D(2,2)
连接CD,∵C(-2,4),∴CD=2![]()
过点D作DH⊥AB,垂足为H,则DH≤CD
当CD⊥AB时,点D到直线AB的距离最大,最大距离为2![]() .
.

 同步拓展阅读系列答案
同步拓展阅读系列答案【题目】已知二次函数![]() 的y与x的部分对应值如表:
的y与x的部分对应值如表:
x | 1 | 0 | 2 | 3 | 4 |
y | 5 | 0 | 4 | 3 | 0 |
下列结论:①抛物线的开口向上;②抛物线的对称轴为直线x=2;③当0<x<4时,y>0;④抛物线与x轴的两个交点间的距离是4;⑤若A(![]() ,2),B(
,2),B(![]() ,3)是抛物线上两点,则
,3)是抛物线上两点,则![]() ,其中正确的个数是 ( )
,其中正确的个数是 ( )
A. 2B. 3C. 4D. 5