ЬтФПФкШн
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
дкбЇЯАЁЖдВЁЗетвЛеТЪБЃЌРЯЪІИјЭЌбЇУЧВМжУСЫвЛЕРГпЙцзїЭМЬтЃК
ГпЙцзїЭМЃКШчЭМЃЌЙ§дВЭтвЛЕузїдВЕФЧаЯп.
вбжЊЃКPЮЊЁбOЭтвЛЕу.
ЧѓзїЃКОЙ§ЕуPЕФЁбOЕФЧаЯп.
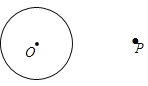
аЁУєЕФзїЗЈШчЯТЃКШчЭМЃЌ
(1)СЌНгOPЃЌзїЯпЖЮOPЕФДЙжБЦНЗжЯпMNНЛOPгкЕуC.
(2)вдЕуCЮЊдВаФЃЌCOЕФГЄЮЊАыОЖзїдВЃЌНЛЁбOгкAЃЌBСНЕу.
(3)зїжБЯпPAЃЌPB.
ЫљвджБЯпPAЃЌPBОЭЪЧЫљЧѓзїЕФЧаЯп.
РЯЪІШЯЮЊаЁУєЕФзїЗЈе§ШЗ.
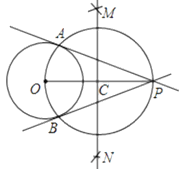
ЧыЛиД№ЃК
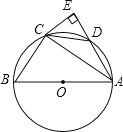
(1)СЌНгOAЃЌOBКѓЃЌПЩжЄЁЯOAPЃНЁЯOBPЃН90ЁуЃЌЦфвРОнЪЧ_________.
(2)ШчЙћЁбOЕФАыОЖЕШгк3ЃЌЕуPЕНЧаЕуЕФОрРыЮЊ4ЃЌЧѓЕуAгыЕуBжЎМфЕФОрРы.
ЁОД№АИЁПЃЈ1ЃЉжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЛЃЈ2ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉжБНгИљОндВжмНЧЖЈРэМДПЩЕУГіЁЯOAP=ЁЯOBP=90ЁуЃЌгЩЧаЯпЕФаджЪМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉСЌНгOA,ABНЛOPгкЕуE,ИљОнЧаЯпЕФаджЪЃЌПЩЕУЁЯOAP =90ЁуЃЌAEЁЭOP,ИљОнЙДЙЩЖЈРэЧѓГіOP,дйИљОнЕШУцЛ§ЗЈЧѓГіAE,МДПЩЧѓГіAB.
ЃЈ1ЃЉНтЃКСЌНгOAЃЌOBКѓЃЌПЩжЄЁЯOAP=ЁЯOBP=90ЁуЃЌЦфвРОнЪЧЃКжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЛ
гЩДЫПЩжЄУїжБЯпPAЃЌPBЖМЪЧЁбOЕФЧаЯпЃЌЦфвРОнЪЧЃКОЙ§АыОЖЭтЖЫЃЌЧвгыАыОЖДЙжБЕФжБЯпЪЧдВЕФЧаЯпЃЎ
ЙЪД№АИЮЊЃКжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЃЛОЙ§АыОЖЭтЖЫЃЌЧвгыАыОЖДЙжБЕФжБЯпЪЧдВЕФЧаЯпЃЎ
ЃЈ2ЃЉСЌНгOA,ABНЛOPгкЕуE,
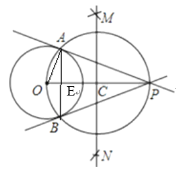
вђЮЊPAЪЧЁбOЕФЧаЯпЃЌ
ЫљвдЁЯOAP =90ЁуЃЌ
дкжБНЧШ§НЧаЮOAPжаЃЌгЩЙДЙЩЖЈРэПЩЕУ:OP=5,
вђЮЊAEЁЭOP,
Ыљвд![]() ,
,
ЫљвдAE=![]() ,
,
ЫљвдAB=![]() .
.