题目内容
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船c的求救信号.已知A、B两船相距100(![]() +3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+3)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
(1)分别求出A与C,A与D之间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距观测点D处200海里范围内有暗礁.若巡逻船A沿直线AC去营救船C,在去营救的途中有无触暗礁危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)

【答案】(1)A与C之间的距离AC为200![]() 海里,A与D之间的距离AD为200(3﹣
海里,A与D之间的距离AD为200(3﹣![]() )海里;(2)巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
)海里;(2)巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.
【解析】
(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,在Rt△AEC中,CE=AEtan60°,在Rt△BCE中,BE=CE=![]() x,由AE+BE=x+
x,由AE+BE=x+![]() x=100(3+
x=100(3+![]() )求出x的值,再根据AC=2x得出AC的值,在△ACD中,由∠DAC=60°,∠ADC=75°得出∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=
)求出x的值,再根据AC=2x得出AC的值,在△ACD中,由∠DAC=60°,∠ADC=75°得出∠ACD=45°.过点D作DF⊥AC于点F,设AF=y,则DF=CF=![]() y,根据AC=y+
y,根据AC=y+![]() y=200
y=200![]() 求出y的值,故可得出AD的长,进而得出结论;
求出y的值,故可得出AD的长,进而得出结论;
(2)根据(1)中的结论得出DF的长,再与200相比较即可.
(1)作CE⊥AB于点E,则∠ABC=45°,∠BAC=60°,设AE=x海里,
∵在Rt△AEC中,CE=AEtan60°=![]() x,
x,
在Rt△BCE中,BE=CE=![]() x,
x,
∴AE+BE=x+![]() x=100(3+
x=100(3+![]() ),解得x=100
),解得x=100![]() ,
,
∴AC=2x=200![]() ,
,
在△ACD中,
∵∠DAC=60°,∠ADC=75°,
∴∠ACD=45°.
过点D作DF⊥AC于点F,设AF=y,则DF=CF=![]() y,
y,
∴AC=y+![]() y=200
y=200![]() ,解得y=100(3﹣
,解得y=100(3﹣![]() ),
),
∴AD=2y=200(3﹣![]() ).
).
答:A与C之间的距离AC为200![]() 海里,A与D之间的距离AD为200(3﹣
海里,A与D之间的距离AD为200(3﹣![]() )海里;
)海里;
(2)∵由(1)可知,DF=![]() AF=
AF=![]() ×100(3﹣
×100(3﹣![]() )≈219,
)≈219,
∵219>200,
∴巡逻船A沿直线AC去营救船C,在去营救的途中无触暗礁危险.

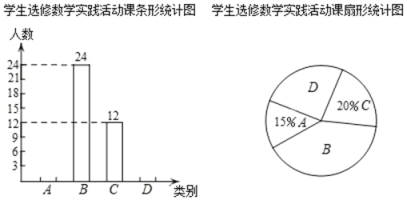
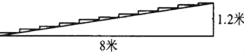
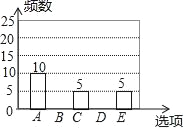
【题目】随着移动终端设备的升级换代,手机已经成为我们生活中不可缺少的一部分,为了解中学生在假期使用手机的情况(选项:A.和同学亲友聊天;B.学习;C.购物;D.游戏;E.其它),端午节后某中学在全校范围内随机抽取了若干名学生进行调查,得到如下图表(部分信息未给出):根据以上信息解答下列问题:
(1)这次被调查的学生有多少人?
(2)求表中m,n,p的值,并补全条形统计图.
(3)若该中学约有800名学生,估计全校学生中利用手机购物或玩游戏的共有多少人?并根据以上调查结果,就中学生如何合理使用手机给出你的一条建议.
选项 | 频数 | 频率 |
A | 10 | m |
B | n | 0.2 |
C | 5 | 0.1 |
D | p | 0.4 |
E | 5 | 0.1 |
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A. 抛物线于x轴的一个交点坐标为(﹣2,0)
B. 抛物线与y轴的交点坐标为(0,6)
C. 抛物线的对称轴是直线x=0
D. 抛物线在对称轴左侧部分是上升的