题目内容
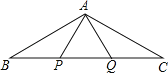
【题目】如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若![]() ,则△A6B6A7的边长为( )
,则△A6B6A7的边长为( )
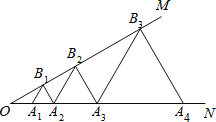
A.6B.12C.16D.32
【答案】C
【解析】
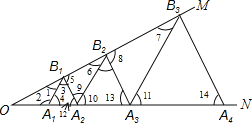
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3,以及A2B2=2B1A2,得出A3B3=4B1A2,A4B4=8B1A2,A5B5=16B1A2…进而得出答案.
解:∵△A1B1A2是等边三角形,
∴A1B1=A2B1,∠3=∠4=∠12=60°,
∴∠2=120°,
∵∠MON=30°,
∴∠1=180°﹣120°﹣30°=30°,
又∵∠3=60°,
∴∠5=180°﹣60°﹣30°=90°,
∵∠MON=∠1=30°,
∴OA1=A1B1=![]() ,
,
∴A2B1=![]() ,
,
∵△A2B2A3、△A3B3A4是等边三角形,
∴∠11=∠10=60°,∠13=60°,
∵∠4=∠12=60°,
∴A1B1∥A2B2∥A3B3,B1A2∥B2A3,
∴∠1=∠6=∠7=30°,∠5=∠8=90°,
∴A2B2=2B1A2,B3A3=2B2A3,
∴A3B3=4B1A2=2,
A4B4=8B1A2=4,
A5B5=16B1A2=8,
…
∴△AnBnAn+1的边长为![]() ×2n﹣1,
×2n﹣1,
∴△A6B6A7的边长为![]() ×26﹣1=
×26﹣1=![]() ×25=16.
×25=16.
故选:C.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目