Question

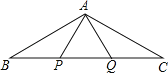
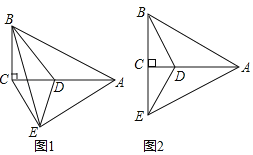
【题目】如图，在Rt△ABC中，∠ACB＝90°，点D在边AC上，将△ABD沿BD（对称轴）翻折，点A落在点E处，连接AE，CE．

（1）如图1，当∠AEC＝90°时，求证：CD＝AD；

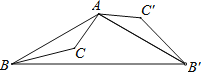
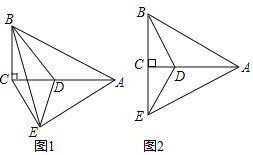
（2）当点E落在BC边所在直线上，且∠AEC＝60°时．

①猜想△BAE是什么三角形并证明；

②试求线段CD、AD之间的数量关系．

Answer 1

【答案】（1）见解析；（2）①△BAE是等边三角形，见解析；②AD＝2CD，见解析

【解析】

（1）先由折叠判断出∠AED＝∠DAE，进而根据∠AEC＝90°得出判断出∠CED+∠AED＝90°，∠DAE+∠ACE＝90°，得出∠CED＝∠ACE，即可得出结论；

（2）①由折叠的性质得出BE＝BA，再利用∠AEC＝60°即可得出结论；

②由折叠得出AD＝DE，∠BED＝∠BAC＝30°，然后由等边三角形的性质得出∠BAC＝30°，进而得出DE＝2CD，即可得出结论．

解：（1）由折叠知，AD＝DE，

∴∠AED＝∠DAE，

∵∠AEC＝90°，

∴∠CED+∠AED＝90°，∠DAE+∠ACE＝90°，

∴∠CED＝∠ACE，

∴CD＝DE，

∵AD＝DE，

∴CD＝AD；

（2）①△BAE是等边三角形，

理由：由折叠知，BE＝BA，

∴△ABE是等腰三角形，

∵点E落在BC边所在直线上，且∠AEC＝60°，

∴△ABE是等边三角形；

②AD＝2CD，理由：

由①知，△ABE是等边三角形，

∴∠BAE＝60°，

∵∠ACB＝90°，

∴∠BAC＝∠BAE＝30°，

由折叠知，AD＝DE，∠BED＝∠BAC＝30°，

在Rt△CDE中，∠BED＝30°，

∴DE＝2CD，

∴AD＝2CD．