题目内容
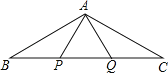
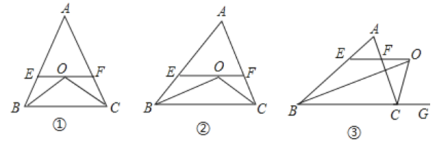
【题目】△ABC中,AB=AC,点D为BC上一点,且DA=DB,此时△ACD也恰好为等腰三角形,则∠BAC=_____.
【答案】90°或108°
【解析】
根据等腰三角形的性质得到∠B=∠C,∠BAD=∠B,由△ACD也恰好为等腰三角形,如图1,当AD=CD,于是得到∠CAD=∠C,求得∠BAC=![]() ×180°=90°,如图2,当AC=CD,根据等腰三角形的性质得到∠CAD=∠ADC,由三角形的外角的性质得到∠ADC=∠B+∠BAD=2∠B,根据三角形的内角和列方程得到∠C+2∠C+2∠C=180°,求得∠C=36°,即可得到结论.
×180°=90°,如图2,当AC=CD,根据等腰三角形的性质得到∠CAD=∠ADC,由三角形的外角的性质得到∠ADC=∠B+∠BAD=2∠B,根据三角形的内角和列方程得到∠C+2∠C+2∠C=180°,求得∠C=36°,即可得到结论.
解:∵AB=AC,
∴∠B=∠C,
∵AD=BD,
∴∠BAD=∠B,
∵△ACD也恰好为等腰三角形,
①如图1,当AD=CD,
∴∠CAD=∠C,
∴∠BAC=![]() ×180°=90°,
×180°=90°,
②如图2,当AC=CD,
∴∠CAD=∠ADC,
∵∠ADC=∠B+∠BAD=2∠B,
∵∠C+∠BAD+∠ADC=180°,
∴∠C+2∠C+2∠C=180°,
∴∠C=36°,
∴∠BAD=36°,∠CAD=72°,
∴∠BAC=108°.
故答案为:90°或108°.



练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目