题目内容
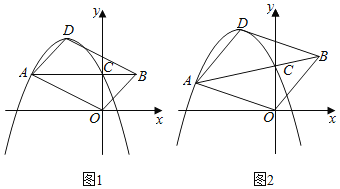
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
【答案】(1)①y=﹣x2﹣2x+1;②证明见解析;(2)存在这样的点A,A(﹣![]() ,
,![]() )
)
【解析】
(1)①由点A(﹣2,1)得到C(0,1),利用待定系数法即可求解;
②作DE⊥x轴于E,交AB于点F,利用顶点坐标及点C的坐标求得DF=![]() ,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
(2)由题意知顶点坐标D(﹣1,c+1),设点A(m,﹣m2﹣2m+c),利用“AAS”证得△AFD≌△BCO,作如图的辅助线,证得△ANF∽△AMC,结合已知![]() =
=![]() ,求得
,求得![]() ,利用比例线段即可求解.
,利用比例线段即可求解.
(1)①∵AC∥x轴,点A(﹣2,1),
∴C(0,1),
将点A(﹣2,1),C(0,1)代入抛物线解析式中,得:
![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+1;
②如图1,过点D作DE⊥x轴于E,交AB于点F,
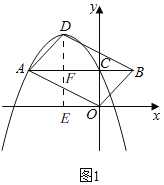
∵AC∥x轴,
∴EF=OC=c,
∵点D是抛物线的顶点坐标,
∴D(![]() ,
,![]() ),
),
∴DF=DE﹣EF=![]() =
=![]() ,
,
∵四边形AOBD是平行四边形,
∴AD=OB,AD∥OB,
∴∠DAF=∠OBC,
∵∠AFD=∠BCO=90°,
∴△AFD≌△BCO(AAS),
∴DF=OC,
∴![]() =c,
=c,
即b2=4c;
(2)如图2,
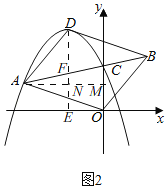
∵b=﹣2.
∴抛物线的解析式为y=﹣x2﹣2x+c,
∴顶点坐标D(﹣1,c+1),
假设存在这样的点A使四边形AOBD是平行四边形,
设点A(m,﹣m2﹣2m+c)(m<0),
过点D作DE⊥x轴于点E,交AB于F,
∴∠AFD=∠EFC=∠BCO,
∵四边形AOBD是平行四边形,
∴AD=BO,AD∥OB,
∴∠DAF=∠OBC,
∴△AFD≌△BCO(AAS),
∴AF=BC,DF=OC,
过点A作AM⊥y轴于M,交DE于N,
∴DE∥CO,
∴△ANF∽△AMC,
∴![]() =
=![]() ,
,
∵AM=﹣m,AN=AM﹣NM=﹣m﹣1,
∴![]() ,
,
∴![]() ,
,
∴点A的纵坐标为﹣(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )+c=c﹣
)+c=c﹣![]() <c,
<c,
∵AM∥x轴,
∴点M的坐标为(0,c﹣![]() ),N(﹣1,c﹣
),N(﹣1,c﹣![]() ),
),
∴CM=c﹣(c﹣![]() )=
)=![]() ,
,
∵点D的坐标为(﹣1,c+1),
∴DN=(c+1)﹣(c﹣![]() )=
)=![]() ,
,
∵DF=OC=c,
∴FN=DN﹣DF=![]() ﹣c,
﹣c,
∵![]() =
=![]() ,
,
∴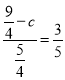 ,
,
∴c=![]() ,
,
∴c﹣![]() =
=![]() ,
,
∴点A纵坐标为![]() ,
,
∴A(﹣![]() ,
,![]() ),
),
∴存在这样的点A,使四边形AOBD是平行四边形.

【题目】为倡导健康环保,自带水杯已成为一种好习惯,某超市销售甲,乙两种型号水杯,进价和售价均保持不变,其中甲种型号水杯进价为25元/个,乙种型号水杯进价为45元/个,下表是前两月两种型号水杯的销售情况:
时间 | 销售数量(个) | 销售收入(元)(销售收入=售价×销售数量) | |
甲种型号 | 乙种型号 | ||
第一月 | 22 | 8 | 1100 |
第二月 | 38 | 24 | 2460 |
(1)求甲、乙两种型号水杯的售价;
(2)第三月超市计划再购进甲、乙两种型号水杯共80个,这批水杯进货的预算成本不超过2600元,且甲种型号水杯最多购进55个,在80个水杯全部售完的情况下设购进甲种号水杯a个,利润为w元,写出w与a的函数关系式,并求出第三月的最大利润.