题目内容
【题目】学校拟购进一批手动喷淋消毒设备,已知1个A型喷雾器和2个B型喷雾器共需90元;2个A型喷雾器和3个B型喷雾器共需165元.
(1)问一个A型喷雾器和一个B型喷雾器的单价各是多少元?
(2)学校决定购进两种型号的喷雾器共60个,并且要求B型喷雾器的数量不能多于A型喷雾器的4倍,请你设计出最为省钱的购买方案,并说明理由.


【答案】(1)一个A型喷雾器的单价为60元,一个B型喷雾器的单价为15元;(2)最省钱的购买方案为:购买A型喷雾器12个,B型喷雾器48个.
【解析】
(1)设一个A型喷雾器的单价为![]() 元,一个B型喷雾器的单价为
元,一个B型喷雾器的单价为![]() 元,根据1个A型喷雾器和2个B型喷雾器共需90元;2个A型喷雾器和3个B型喷雾器共需165元列出方程组进行求解即可;
元,根据1个A型喷雾器和2个B型喷雾器共需90元;2个A型喷雾器和3个B型喷雾器共需165元列出方程组进行求解即可;
(2)设购进A型喷雾器![]() 个,则购进B型喷雾器
个,则购进B型喷雾器![]() 个,根据题意先求出m的取值范围,再设这些喷雾器的总费用为W元,得到W关于m的函数解析式,利用一次函数的性质进行求解即可.
个,根据题意先求出m的取值范围,再设这些喷雾器的总费用为W元,得到W关于m的函数解析式,利用一次函数的性质进行求解即可.
(1)设一个A型喷雾器的单价为![]() 元,一个B型喷雾器的单价为
元,一个B型喷雾器的单价为![]() 元,由题意可得:
元,由题意可得:
![]()
解之得:![]() ,
,
答:一个A型喷雾器的单价为60元,一个B型喷雾器的单价为15元;
(2)设购进A型喷雾器![]() 个,则购进B型喷雾器
个,则购进B型喷雾器![]() 个,由题意可得:
个,由题意可得:
![]() ≤
≤![]()
解之得:![]() ≥12
≥12
设购买这些喷雾器的总费用为W元,则有:
![]()
∵![]()
∴W随![]() 的增大而增大
的增大而增大
∴当![]() 时,W取得最小值,及最省钱.
时,W取得最小值,及最省钱.
![]() (个)
(个)
答:最省钱的购买方案为:购买A型喷雾器12个,B型喷雾器48个.

 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案【题目】某中学开展普通话演讲比赛,九(1)、(2)两个班根据初赛成绩各选出5名选手参加复赛,10名选手的复赛成绩如图所示:
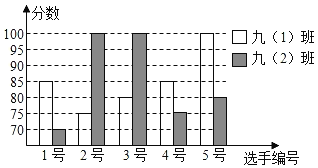
(1)根据如图补充完成下面的成绩统计分析表:
平均数 | 中位数 | 众数 | 方差 | 合格率 | 优秀率 | |
九(1)班 | 85 |
| 85 |
|
| 60% |
九(2)班 | 85 | 80 |
| 160 | 100% |
|
(2)九(1)班学生说他们的复赛成绩好于九(2)班,结合图表,请你给出三条支持九(1)班学生观点的理由.
(3)如果从复赛成绩100分的3名选手中任选2人参加学校决赛,求选中的两位选手恰好一位来自于九(1)班,另一位来自于九(2)班的概率.
【题目】某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量y(千克)与每千克售价x(元)满足一次函数关系,部分数据如下表:
售价x(元/千克) | 50 | 60 | 70 |
销售量y(千克) | 100 | 80 | 60 |
(1)求y与x之间的函数表达式;
(2)设商品每天的总利润为W(元),则当售价x定为多少元时,厂商每天能获得最大利润?最大利润是多少?
(3)如果超市要获得每天不低于1350元的利润,且符合超市自己的规定,那么该商品每千克售价的取值范围是多少?请说明理由.