题目内容
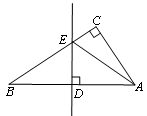
如图,在△ABC中,已知AB=BC=AC=4cm,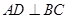 于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为t(s),
于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为t(s),
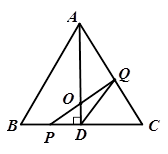
(1)求t为何值时,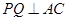 ;
;
(2)当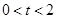 时,求证:AD平分△PQD的面积;
时,求证:AD平分△PQD的面积;
(3)当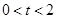 时,求△PQD面积的最大值.
时,求△PQD面积的最大值.
 于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为t(s),
于D,点P、Q分别从B、C两点同时出发,其中点P沿BC向终点C运动,速度为1cm/s,点Q沿CA,AB向终点B运动,速度为2cm/s,设它们运动的时间为t(s),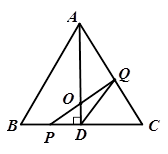
(1)求t为何值时,
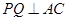 ;
;(2)当
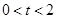 时,求证:AD平分△PQD的面积;
时,求证:AD平分△PQD的面积;(3)当
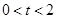 时,求△PQD面积的最大值.
时,求△PQD面积的最大值.(1)当t=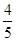 (Q在AC上)时,
(Q在AC上)时,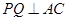 ;
;
(2)证明见解析;
(3)当t=1时,△PQD面积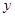 的最大值为
的最大值为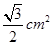 .
.
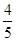 (Q在AC上)时,
(Q在AC上)时,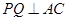 ;
;(2)证明见解析;
(3)当t=1时,△PQD面积
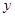 的最大值为
的最大值为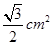 .
.试题分析:(1)若使PQ⊥AC,则根据路程=速度×时间表示出CP和CQ的长,再根据30度的直角三角形的性质列方程求解;
(2)根据三角形的面积公式,要证明AD平分△PQD的面积,只需证明O是PQ的中点.根据题意可以证明BP=CN,则PD=DN,再根据平行线等分线段定理即可证明;
(3)△PQD面积与t的函数关系式,再求最大值即可.
试题解析:(1)当Q在AB上时,显然不存在
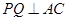 ;
;当Q在AC上时,BP=t,CQ=2x,PC=4-t
∵AB=BC=AC=4cm,
∴∠C=60°
若
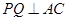 ,则∠QPC=30°
,则∠QPC=30°∴PC=2QC,
∴4-t=2×2t,
∴t=
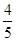 ,
,当t=
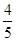 (Q在AC上)时,
(Q在AC上)时,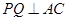 ;
;(2)过点Q作QE⊥BC于点E,
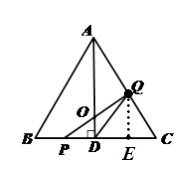
∵∠ODP=90°=∠QEP,∠OPD=∠QPD
∴△ODP∽△QEP
∴
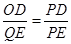
∵当
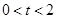 时,BP=t, PD="2-t" ,
时,BP=t, PD="2-t" ,又CQ=2t,CE=t,PE=BC-BP-CE=4-t-t=4-2t
∴PD=
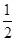 PE,
PE,∴OD=
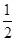 QE
QE∵
 ,
,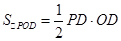
∴
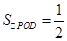
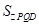 ,
,∴AD平分△PQD的面积;
(3)当
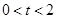 时,设△PQD面积为
时,设△PQD面积为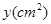 ,
,∵PD="2-t" ,QE=
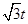
∴
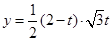 =
=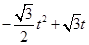 =
=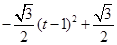
∴当t=1时,△PQD面积
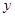 的最大值为
的最大值为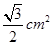 .
.
练习册系列答案
相关题目
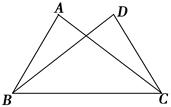
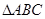 中
中 是腰
是腰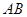 的垂直平分线,
的垂直平分线,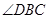 的度数是 。
的度数是 。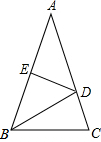
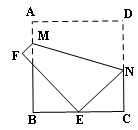
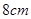 的正方形
的正方形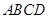 折叠,使点
折叠,使点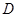 落在
落在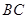 边中点
边中点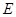 处,点
处,点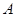 落在点
落在点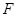 处,折痕为
处,折痕为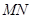 ,则
,则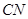 的长为 .
的长为 .