题目内容
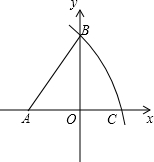
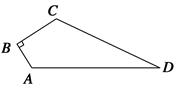
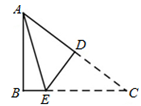
如图1，M是铁丝AD的中点，将该铁丝首尾相接折成△ABC，且∠B=30°，∠C=100°，如图2．则下列说法正确的是（ ）
| A．点M在AB上 |
| B．点M在BC的中点处 |
| C．点M在BC上，且距点B较近，距点C较远 |
| D．点M在BC上，且距点C较近，距点B较远 |
C
本题考查了三角形的三边关系，作辅助线把△ABC的周长分成两个部分是解题的关键，根据钝角三角形中钝角所对的边最长可得AB＞AC，取BC的中点E，求出AB+BE＞AC+CE，再根据三角形的任意两边之和大于第三边得到AB＜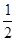
AD，从而判定AD的中点M在BE上．
解：∵∠C=100°，
∴AB＞AC，
如图，取BC的中点E，则BE=CE，
∴AB+BE＞AC+CE，
由三角形三边关系，AC+BC＞AB，
∴AB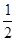＜AD，
∴AD的中点M在BE上，
即点M在BC上，且距点B较近，距点C较远．
故选C．
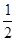AD，从而判定AD的中点M在BE上．解：∵∠C=100°，
∴AB＞AC，
如图，取BC的中点E，则BE=CE，
∴AB+BE＞AC+CE，
由三角形三边关系，AC+BC＞AB，
∴AB＜
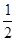AD，∴AD的中点M在BE上，
即点M在BC上，且距点B较近，距点C较远．
故选C．
练习册系列答案
相关题目
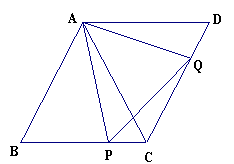
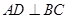于D，点P、Q分别从B、C两点同时出发，其中点P沿BC向终点C运动，速度为1cm/s，点Q沿CA，AB向终点B运动，速度为2cm/s，设它们运动的时间为t(s)，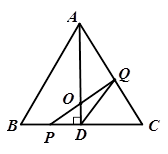
；
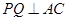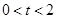时，求证：AD平分△PQD的面积；
