题目内容
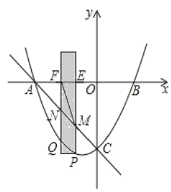
【题目】在矩形![]() 中,
中,![]() 为
为![]() 边上一点
边上一点![]() ,
,![]() .将
.将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,![]() 的延长线交边
的延长线交边![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .连接
.连接![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() .现有以下结论:①连接
.现有以下结论:①连接![]() ,则
,则![]() 垂直平分
垂直平分![]() ;②四边形
;②四边形![]() 是菱形;③
是菱形;③![]() ;④若
;④若![]() ,则
,则![]() .其中正确的结论是________(填写所有正确结论的序号).
.其中正确的结论是________(填写所有正确结论的序号).
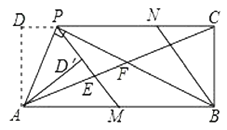
【答案】①②③
【解析】
①连接![]() ,根据翻折的性质,结合等腰三角形三线合一的性质即可得出结论;
,根据翻折的性质,结合等腰三角形三线合一的性质即可得出结论;
②DP∥AB,所以∠DPA=∠PAM,由题意可知:∠DPA=∠APM,所以∠PAM=∠APM,由于∠APB-∠PAM=∠APB-∠APM,即∠ABP=∠MPB,从而可知PM=MB=AM,又易证四边形PMBN是平行四边形,所以四边形PMBN是菱形;
③过点P作PG⊥AB于点G,易知四边形DPGA,四边形PCBG是矩形,所以AD=PG,DP=AG,GB=PC,易证△APG∽△PBG,所以PG2=AGGB,即AD2=DPPC;
④由于![]() ,可设DP=1,AD=2,由(1)可知:AG=DP=1,PG=AD=2,从而求出GB=PC=4,AB=AG+GB=5,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得
,可设DP=1,AD=2,由(1)可知:AG=DP=1,PG=AD=2,从而求出GB=PC=4,AB=AG+GB=5,由于CP∥AB,从而可证△PCF∽△BAF,△PCE∽△MAE,从而可得![]() ,
,![]() ,从而可求出EF=AF-AE=
,从而可求出EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,从而可得
AC,从而可得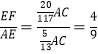 .
.
①根据翻折的性质可得,AD=A![]() ,∠DAP=∠
,∠DAP=∠![]() AP,
AP,
连接![]() ,根据等腰三角形“三线合一”的性质得,
,根据等腰三角形“三线合一”的性质得,![]() 垂直平分
垂直平分![]() .
.
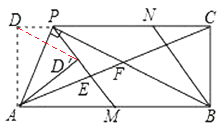
②∵DP∥AB,
∴∠DPA=∠PAM,
由题意可知:∠DPA=∠APM,
∴∠PAM=∠APM,
∵∠APB-∠PAM=∠APB-∠APM,
即∠ABP=∠MPB
∴AM=PM,PM=MB,
∴PM=MB,
又易证四边形PMBN是平行四边形,
∴四边形PMBN是菱形;
③过点P作PG⊥AB于点G,
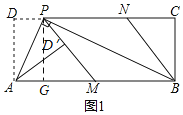
∴易知四边形DPGA,四边形PCBG是矩形,
∴AD=PG,DP=AG,GB=PC
∵∠APB=90°,
∴∠APG+∠GPB=∠GPB+∠PBG=90°,
∴∠APG=∠PBG,
∴△APG∽△PBG,
∴![]() ,
,
∴PG2=AGGB,
即AD2=DPPC;
④由于![]() ,
,
可设DP=1,AD=2,
由(1)可知:AG=DP=1,PG=AD=2,
∵PG2=AGGB,
∴4=1GB,
∴GB=PC=4,
AB=AG+GB=5,
∵CP∥AB,
∴△PCF∽△BAF,
∴![]() ,
,
∴![]() ,
,
又易证:△PCE∽△MAE,AM=![]() AB=
AB=![]() ,
,
∴![]()
∴![]() ,
,
∴EF=AF-AE=![]() AC-
AC-![]() AC=
AC=![]() AC,
AC,
∴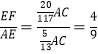 .
.
故答案为:①②③.