题目内容
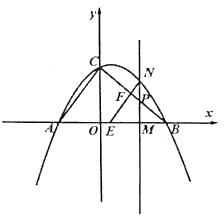
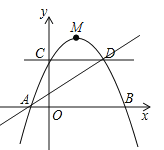
【题目】如图,已知顶点为![]() 的抛物线过点
的抛物线过点![]() ,交
,交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() ,点
,点![]() 是抛物线上一动点.
是抛物线上一动点.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当点
当点![]() 在直线
在直线![]() 上方时,求
上方时,求![]() 面积的最大值,并求出此时点
面积的最大值,并求出此时点![]() 的坐标;
的坐标;
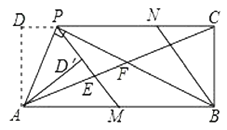
![]() 过点
过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,若将
,若将![]() 沿
沿![]() 翻折点
翻折点![]() 的对应点为点
的对应点为点![]() .是否存在点
.是否存在点![]() ,使
,使![]() 恰好落在
恰好落在![]() 轴上?若存在,求出点
轴上?若存在,求出点![]() 的坐标:若不存在,说明理由.
的坐标:若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() 有最大值
有最大值![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ;(3)存在,
;(3)存在,
【解析】
(1)先设设抛物线解析式为 ,然后用待定系数法求解即可;
,然后用待定系数法求解即可;
(2)由S△PAD=S△PHA+S△PHD,然后将S△PAD表示出来,最后求最值即可;
(3)设点P的坐标为点![]() 的坐标为
的坐标为![]() ,然后分当P点在y轴右侧或左侧两种情况,分别运用解直角三角形以及相似三角形的性质求解即可.
,然后分当P点在y轴右侧或左侧两种情况,分别运用解直角三角形以及相似三角形的性质求解即可.
解:![]() 根据题意设抛物线解析式为
根据题意设抛物线解析式为

把点![]() 的坐标代入得
的坐标代入得![]()
解得![]()
所以抛物线解析式为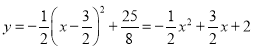 ;
;
![]() 如图,由已知抛物线过点
如图,由已知抛物线过点![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]()
所以可得![]() 的坐标为,
的坐标为,![]()
且![]() 轴设经过
轴设经过![]() 两点的直线
两点的直线![]() 的解析式为
的解析式为![]()
把![]() 的坐标代入得
的坐标代入得![]()
解得![]()
所以直线![]() 的解析式为
的解析式为![]()
过点![]() 作
作![]() 轴的垂线,分别交
轴的垂线,分别交![]() 轴于点
轴于点![]() ,连结
,连结![]()
因为点![]() 在抛物线上,故设点
在抛物线上,故设点![]() 的坐标为
的坐标为![]()
则点![]() 的坐标为
的坐标为![]()
所以![]()
所以![]()
![]()
![]()
![]()
![]()
当![]() 时,
时,![]() 有最大值
有最大值![]() ,此时点
,此时点![]() 的坐标为
的坐标为![]() ;
;
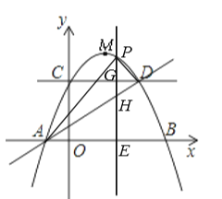
![]() 存在满足条件的点
存在满足条件的点![]() ,显然点
,显然点![]() 在直线
在直线![]() 下方.
下方.
设直线![]() 交
交![]() 轴于
轴于![]() ,点
,点![]() 的坐标为
的坐标为![]()
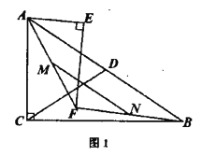
① 当点![]() 在
在![]() 轴右侧(如图 ),
轴右侧(如图 ),![]()
![]()
又![]() ,
,![]()
![]()
![]()
![]()
即
解得![]()
![]()
![]()
此时![]() ,点
,点![]() 的坐标为
的坐标为

② 当点![]() 在
在![]() 轴左侧时(如图 2)此时
轴左侧时(如图 2)此时![]() ,
,![]()
![]()
又![]() ,
,![]()
![]()
![]()
即
解得![]()
![]()
![]()
此时![]() ,点
,点![]() 的坐标为
的坐标为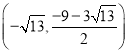
综上所述,满足条件的点![]() 坐标为
坐标为
 .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目