题目内容
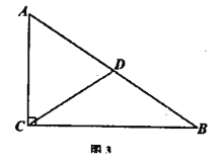
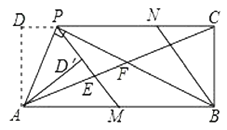
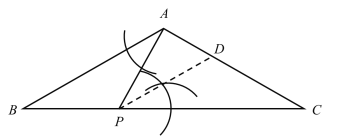
【题目】如图,在△ABC中,AB=AC,点P在BC上.
(1)求作:△PCD,使点D在AC上,且△PCD∽△ABP;(要求:尺规作图,保留作图痕迹,不写作法)
(2)在(1)的条件下,若∠APC=2∠ABC,求证:PD//AB.

【答案】(1)见解析;(2)见解析
【解析】
(1)根据相似三角形的性质可得∠CPD=∠BAP,故作∠CPD=∠BAP,∠CPD与AC的交点为D即可;
(2)利用外角的性质以及(1)中∠CPD=∠BAP可得∠CPD =∠ABC,再根据平行线的判定即可.
解:(1)∵△PCD∽△ABP,
∴∠CPD=∠BAP,
故作∠CPD=∠BAP即可,
如图,即为所作图形,
(2)∵∠APC=∠APD+∠DPC=∠ABC+∠BAP=2∠ABC,
∴∠BAP =∠ABC,
∴∠BAP=∠CPD=∠ABC,
即∠CPD =∠ABC,
∴PD∥AB.

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目