Question

【题目】如图，某中心广场灯柱AB被钢缆CD固定，已知CB=5米，且sin∠DCB＝．

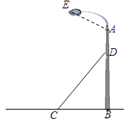
（1）求钢缆CD的长度。

（2）若AD=2米，灯的顶端E距离A处1.6米，且∠EAB=120°，则灯的顶端E距离地面多少米？

Answer 1

【答案】（1）CD=米；（2）．

【解析】

试题 （1）根据三角函数可求得CD；

（2）过点E作EF⊥AB于点F．由∠EAB=120°，得∠EAF=60°，再根据三角函数求得AF，从而得出答案．

试题解析：（1）在Rt△DCB中，sin∠DCB==，∴设DB=4x，DC=5x，由勾股定理得：∴，解得或（舍），∴CD=米，DB=米；

（2）如图，过点E作EF⊥AB于点F，∵∠EAB＝120°，∴∠EAF＝60°，∴AF＝AE·cos∠EAF=1.6×=0.8（米），∴FB＝AF＋AD＋DB=0.8＋2＋=（米），∴灯的顶端E距离地面米．