题目内容
【题目】如图,![]() ,
,![]() ,
,![]() 三点在
三点在![]() 上,直径
上,直径![]() 平分
平分![]() ,过点
,过点![]() 作
作![]() 交弦
交弦![]() 于点
于点![]() ,在
,在![]() 的延长线上取一点
的延长线上取一点![]() ,使得
,使得![]() .
.
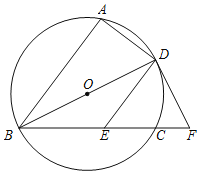
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)连接AF交DE于点M,若AD=4,DE=5,求DM的长.
【答案】(1)见解析;(2)1
【解析】
(1)先得出∠ABD=∠CBD,进而得出OD⊥DF,即可得出结论;
(2)连接DC,利用全等三角形的判定得出△ABD≌△CBD,进而解答即可.
(1)证明:∵BD平分∠ABC,
∴∠ABD=∠CBD.
∵DE∥AB,
∴∠ABD=∠BDE.
∴∠CBD=∠BDE.
∵ED=EF,
∴∠EDF=∠EFD.
∵∠EDF+∠EFD+∠EDB+∠EBD=180°,
∴∠BDF=∠BDE+∠EDF=90°.
∴OD⊥DF.
∵OD是半径,
∴DF是⊙O的切线.
(2)解:连接DC,
∵BD是⊙O的直径,
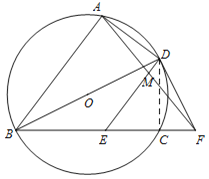
∴∠BAD=∠BCD=90°.
∵∠ABD=∠CBD,BD=BD,
∴△ABD≌△CBD.
∴CD=AD=4,AB=BC.
∵DE=5,
∴CE=![]() =3,EF=DE=5.
=3,EF=DE=5.
∵∠CBD=∠BDE,
∴BE=DE=5.
∴BF=BE+EF=10,BC=BE+EC=8.
∴AB=8.
∵DE∥AB,
∴△ABF∽△MEF.
∴![]() .
.
∴ME=4.
∴DM=DE-EM=1.

练习册系列答案
相关题目