题目内容
(5分)第一象限内的点A在某一反比例函数的图象上,过A作AB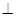 x轴,垂足为B,连接AO,已知△AOB的面积为4.
x轴,垂足为B,连接AO,已知△AOB的面积为4.
小题1: ⑴求反比例函数的解析式
小题2:⑵若点A的纵坐标为4,过点A的直线与x轴交于P(不与点B、O重合),且以A、P、B为顶点的三角形与△AOB相似,写出符合条件的点P的坐标.
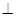 x轴,垂足为B,连接AO,已知△AOB的面积为4.
x轴,垂足为B,连接AO,已知△AOB的面积为4.小题1: ⑴求反比例函数的解析式
小题2:⑵若点A的纵坐标为4,过点A的直线与x轴交于P(不与点B、O重合),且以A、P、B为顶点的三角形与△AOB相似,写出符合条件的点P的坐标.

小题1:(1) y=
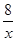
小题2:(2)p(4,0) 或(10,0) 或(﹣6,0) ……………………5分
(1)利用反比例函数的性质即可得出k的值,即可得出答案;
(2)首先得出A点的坐标,再利用当△ABP∽△ABO时,以及当△PBA∽△ABO时,分别求出即可;

点A的坐标为(x,y),
∵S△AOB=4,
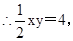
∴xy=8,
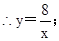
(2)由题意得A(2,4),
∴B(2,0),
∵点P在x轴上,设P点坐标为(x,0),
∴∠ABO=∠ABP=90°,
∴△ABP与△ABO相似有两种情况:
①当△ABP∽△ABO时,
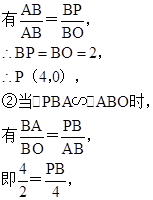
∴PB=8,
∴P(10,0)或P(-6,0);
∴符合条件的点P坐标是(4,0)或(10,0)或(-6,0);

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
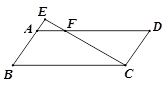

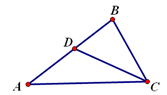
 BC。
BC。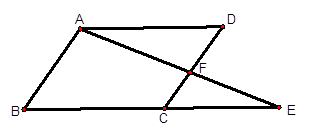
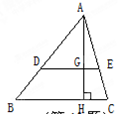
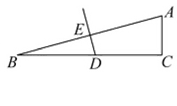
 的值.
的值.
 ,且BD=2,AD=3,求BC的长。
,且BD=2,AD=3,求BC的长。