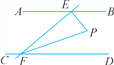
题目内容
【题目】如图,∠EOF=90°,点A,B分别在射线OE,OF上移动,连结AB并延长至点D,∠DBO的平分线与∠OAB的平分线交于点C,试问:∠ACB的大小是否随点A,B的移动而发生变化?如果保持不变,请说明理由;如果随点A,B的移动而发生变化,请给出变化的范围.
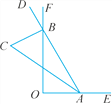
【答案】∠ACB不随点A,B的移动发生变化
【解析】试题分析:∠ACB不随点A,B的移动发生变化,根据角平分线的定义、三角形外角的性质、三角形的内角和定理解决即可.
试题解析:
∠ACB不随点A,B的移动发生变化.理由如下:
∵BC,AC分别平分∠DBO,∠BAO,
∴∠DBC=![]() ∠DBO,∠BAC=
∠DBO,∠BAC=![]() ∠BAO.
∠BAO.
∵∠DBO+∠OBA=180°,∠OBA+∠BAO+∠AOB=180°,
∴∠DBO=∠BAO+∠AOB,
∴∠DBO-∠BAO=∠AOB=90°.
∵∠DBC+∠ABC=180°,∠ABC+∠ACB+∠BAC=180°,
∴∠DBC=∠BAC+∠ACB,
∴![]() ∠DBO=
∠DBO=![]() ∠BAO+∠ACB,
∠BAO+∠ACB,
∴∠ACB=![]() (∠DBO-∠BAO)=
(∠DBO-∠BAO)=![]() ∠AOB=45°.
∠AOB=45°.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目