题目内容
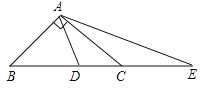
【题目】如图,△ABC中,边AB、AC的垂直平分线分别交BC于D、E.
(1)若BC=10,则△ADE周长是多少?为什么?
(2)若∠BAC=128°,则∠DAE的度数是多少?为什么?

【答案】(1)10;(2)76°理由见解析
【解析】试题分析:(1)根据垂直平分线性质得AD=BD,AE=EC.所以△ADE周长=BC;
(2)∠DAE=∠BAC﹣(∠BAD+∠CAE).根据三角形内角和定理及等腰三角形性质求解.
解:(1)C△ADE=10.
∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE.
C△ADE=AD+DE+AE=BD+DE+CE=BC=10.
(2)∠DAE=76°.
∵AB、AC的垂直平分线分别交BC于D、E,
∴AD=BD,AE=CE.
∴∠B=∠BAD,∠C=∠CAE.
∵∠BAC=128°,
∴∠B+∠C=52°.
∴∠DAE=∠BAC﹣(∠BAD+∠CAE)
=∠BAC﹣(∠B+∠C)=76°.

练习册系列答案
相关题目
【题目】下表反映的是某地区电的使用量x(千瓦时)与应交电费y(元)之间的关系,下列说法不正确的是( )
用电量x(千瓦时) | 1 | 2 | 3 | 4 | … |
应交电费y(元) | 0.55 | 1.1 | 1.65 | 2.2 | … |
A. x与y都是变量,且x是自变量,y是函数
B. 用电量每增加1千瓦时,电费增加0.55元
C. 若用电量为8千瓦时,则应交电费4.4元
D. y是x的反比例函数