题目内容
【题目】已知：点
，
.
（1）求：直线
的表达式；
（2）直接写出直线向下平移2个单位后得到的直线表达式；
（3）求：在（2）的平移中直线在第三象限内扫过的图形面积.
【答案】（1）
；（2）
；（3）
.
【解析】
（1）根据点
、
的坐标利用待定系数法即可求出直线
的表达式；
（2）根据平移的规律“上加下减，左加右减”即可得出平移后的直线表达式；
（3）设直线与
轴交点为点
，与
轴的交点为点
，根据一次函数图象上点的坐标特征可求出点、的坐标，再根据直线在第三象限内扫过的图形面积
结合三角形的面积公式即可得出结论．
解：（1）设直线的表达式为
，
将
，
代入，
得
，解得：
，
∴直线的表达式为.
（2）根据平移的规律可知：直线：向下平移2个单位后得到的直线表达式为：
.
（3）设直线与轴交点为点，与轴的交点为点，
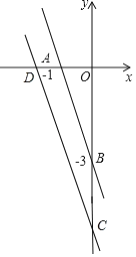
在中，当
时，
，
∴点的坐标为
；
当
时，
，
∴点的坐标为
．
∴直线在第三象限内扫过的图形面积,
,
.
练习册系列答案
名校课堂系列答案
相关题目
【题目】一定数量的石子可以摆成如图所示的三角形和四边形，古希腊科学家把1,3,6,10,15,21，…，称为“三角形数”；把1,4,9,16,25，…，称为“正方形数”.
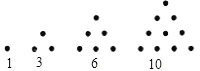
将三角形、正方形、五边形都整齐的由左到右填在所示表格里：
三角形数 | 1 | 3 | 6 | 10 | 15 | 21 | a | … |
正方形数 | 1 | 4 | 9 | 16 | 25 | b | 49 | … |
五边形数 | 1 | 5 | 12 | 22 | C | 51 | 70 | … |
（1）按照规律，表格中a=___，b=___，c=___．
（2）观察表中规律，第n个“正方形数”是________；若第n个“三角形数”是x，则用含x、n的代数式表示第n个“五边形数”是___________．
