题目内容
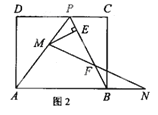
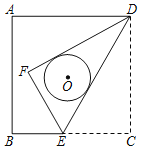
【题目】如图,已知边长为2的正方形ABCD,边BC上有一点E,将△DCE沿DE折叠至△DFE,若DF,DE恰好与以正方形ABCD的中心为圆心的⊙O相切,则⊙O的半径为_____.
【答案】![]() .
.
【解析】
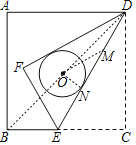
连接BD交于点O,设ED与⊙O相切于点N,连接ON,由O为正方形的中心,得到∠ADO=∠CDO,又DF与DE为圆O的切线,根据切线长定理得到DO平分∠EDF,可得出∠ADF=∠CDE,由折叠可得∠CDE=∠FDE,再由正方形的内角为直角,可得出∠EDC为30°,在DN上取点M,使OM=DM,则∠OMN=30°,在直角三角形DON中,可求出NO的长.
解:连接BD交于点O,设ED与⊙O相切于点N,连接ON,
∵O为正方形ABCD的中心,
∴∠ADO=∠CDO,
又∵DF与DE都为圆O的切线,
∴DO平分∠EDF,即∠ODF=∠ODE,
∴∠ADO﹣∠FDO=∠CDO﹣∠ODE,即∠ADF=∠CDE,
又∵△DCE沿着DE折叠至△DFE,
∴∠CDE=∠EDF,
∴∠CDE=∠EDF=∠ADF=![]() ∠ADC=30°,
∠ADC=30°,
∴∠ODN=15°,
∵BC=CD=2,
∴DO=![]() BD=
BD=![]() ,
,
在DN上取点M,使OM=DM,则∠OMN=30°,
设ON=x,则OM=DM=2x,MN=![]() x,
x,
在Rt△DON中,ON2+DN2=OD2,
∴![]() ,
,
∴![]() .
.
∴![]() .
.
故答案为:![]() .
.

练习册系列答案
相关题目