题目内容
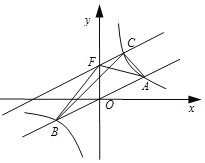
【题目】如图,在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 、
、![]() 两点,且点
两点,且点![]() 的坐标为
的坐标为![]() ,将直线
,将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,且
,且![]() 的面积是
的面积是![]() .给出以下结论:(1)
.给出以下结论:(1)![]() ;(2)点
;(2)点![]() 的坐标是
的坐标是![]() ;(3)
;(3)![]() ;(4)
;(4)![]() .其中正确的结论有
.其中正确的结论有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
【答案】C
【解析】
(1)把A(4,a)代入![]() ,求得A为(4,2),然后代入
,求得A为(4,2),然后代入![]() 求得k=8;
求得k=8;
(2)联立方程,解方程组即可求得B(-4,-2);
(3)根据同底等高的三角形相等,得出S△ABC=S△ABF;
(4)根据S△ABF=S△AOF+S△BOF列出![]() ,解得
,解得![]() 。
。
解:(1)![]() 直线
直线![]() 经过点
经过点![]() ,
,
![]() ,
,
![]() ,
,
![]() 点
点![]() 在双曲线
在双曲线![]() 上,
上,
![]() ,故正确;
,故正确;
(2)解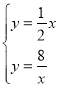 得
得![]() 或
或![]() ,
,
![]() 点
点![]() 的坐标是
的坐标是![]() ,故正确;
,故正确;
(3)![]() 将直线
将直线![]() 向上平移
向上平移![]() 个单位,交双曲线
个单位,交双曲线![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
![]() ,
,
![]() 和
和![]() 是同底等高,
是同底等高,
![]() ,故错误;
,故错误;
(4)![]() ,
,
![]() ,
,
解得![]() ,故正确;
,故正确;
故选:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目