题目内容
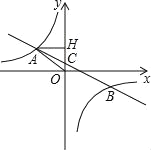
【题目】在平面直角坐标系xOy中，A（﹣3，2），B（0，1），将线段AB沿x轴的正方向平移n（n＞0）个单位，得到线段A′，B′恰好都落在反比例函数y
（m≠0）的图象上．
（1）用含n的代数式表示点A′，B′的坐标；
（2）求n的值和反比例函数y（m≠0）的表达式；
（3）点C为反比例函数y（m≠0）图象上的一个动点，直线CA′与x轴交于点D，若CD＝2A′D，请直接写出点C的坐标．
【答案】（1）A′（n﹣3，2），B′（n，1）；（2）n的值为6，反比例函数的表达式为y
；（3）点C的坐标为（
，4）或（
，﹣4）．
【解析】
（1）利用平移的性质，可用含n的代数式表示点A′，B′的坐标；
（2）根据点A′，B′的坐标，利用待定系数法可得出关于m，n的方程组，解之即可得出结论；
（3）过点C作CE⊥x轴于点E，过点A′作A′F⊥x轴于点F，则△A′DF∽△CDE，利用相似三角形的性质可得出CE的值，再利用反比例函数图象上点的坐标特征可求出点C的坐标．
解：（1）∵点A（﹣3，2）沿x轴的正方向平移n（n＞0）个单位得到点A′，
∴点A′的坐标为（n﹣3，2）．
同理，可得出：点B′的坐标为（n，1）．
（2）将A′（n﹣3，2），B′（n，1）代入y
，得：
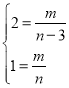，解得：
，
∴n的值为6，反比例函数的表达式为y
．
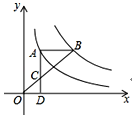
（3）过点C作CE⊥x轴于点E，过点A′作A′F⊥x轴于点F，如图所示．
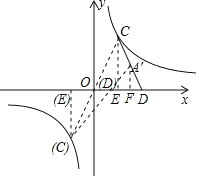
∵A′F∥CE，
∴△A′DF∽△CDE，
∴
，即
，
∴CE＝4．
当y＝4时，x
，
此时点C的坐标为（
，4）；
当y＝﹣4时，x
，
此时点C的坐标为（
，﹣4）．
综上所述：点C的坐标为（，4）或（，﹣4）．
练习册系列答案
名校课堂系列答案
相关题目
