题目内容
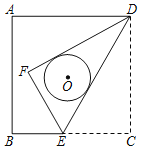
【题目】如图,在Rt△ABC中,∠ABC=90°.AB=BC.点D是线段AB上的一点,连结CD.过点B作BG⊥CD,分别交CD、CA于点E、F,与过点A且垂直于AB的直线相交于点G,连结DF,给出以下四个结论:①![]() ;②若点D是AB的中点,则AF=
;②若点D是AB的中点,则AF=![]() AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若
AB;③当B、C、F、D四点在同一个圆上时,DF=DB;④若![]() ,则S△ABC=9S△BDF,其中正确的结论序号是______.
,则S△ABC=9S△BDF,其中正确的结论序号是______.
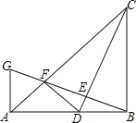
【答案】①②③
【解析】
由△AFG∽△CFB,可确定结论①正确;由△ABG≌△BCD可得AG=![]() AB=
AB=![]() BC,进而由△AFG∽△CFB确定点F为AC的三等分点,可确定结论②正确;当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠CFD=∠ABC=90°,得到CD为圆的直径,因为BG⊥CD,根据垂径定理得到DF=DB,故③正确;因为D为AB的三等分点,△AFG∽△CFB,所以
BC,进而由△AFG∽△CFB确定点F为AC的三等分点,可确定结论②正确;当B、C、F、D四点在同一个圆上时,由圆内接四边形的性质得到∠CFD=∠ABC=90°,得到CD为圆的直径,因为BG⊥CD,根据垂径定理得到DF=DB,故③正确;因为D为AB的三等分点,△AFG∽△CFB,所以![]() 所以S△ABF=
所以S△ABF=![]() S△ABC,又S△BDF=
S△ABC,又S△BDF=![]() S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.
S△ABF,所以S△ABC=12S△BDF,由此确定结论④错误.
解:依题意可得BC∥AG,
∴△AFG∽△CFB,
∴![]() ,
,
又AB=BC,
∴![]() .故结论①正确;
.故结论①正确;
如图,
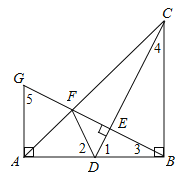
∵∠1+∠3=90°,∠1+∠4=90°,
∴∠3=∠4.
在△ABG与△BCD中,
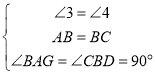 ,
,
∴△ABG≌△BCD(ASA),
∴AG=BD,
又∵BD=AD,
∴AG=AD;
∵△ABC为等腰直角三角形,
∴AC=![]() AB;
AB;
∴AG=AD=![]() AB=
AB=![]() BC;
BC;
∵△AFG∽△BFC,
∴![]() ,
,
∴FC=2AF,
∴AF=![]() AC=
AC=![]() AB.故结论②正确;
AB.故结论②正确;
当B、C、F、D四点在同一个圆上时,
由圆内接四边形的性质可得∠CFD=∠ABC=90°
∴CD是B、C、F、D四点所在圆的直径,
∵BG⊥CD,
∴![]() ,
,
∴DF=DB,故③正确;
∵![]() ,AG=BD,
,AG=BD,![]() ,
,
∴![]() ,
,
∴S△BDF=![]() S△ABF,
S△ABF,![]() ,
,
∴AF=![]() AC,
AC,
∴S△ABF=![]() S△ABC;
S△ABC;
∴S△BDF=![]() S△ABC,即S△ABC=12S△BDF.故结论④错误.
S△ABC,即S△ABC=12S△BDF.故结论④错误.
∴正确的结论有①②③;
故答案为:①②③.