Question

【题目】定义：圆心在三角形的一边上，与另一边相切，且经过三角形一个顶点（非切点）的圆，称为这个三角形圆心所在边上的“友好圆”．

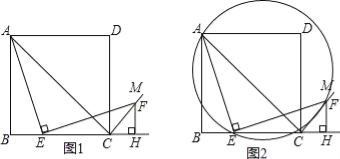
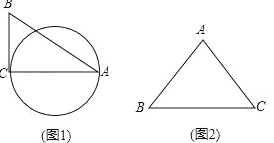
（1）如图1，△ABC中，∠C=90°，AB=13，BC=5，则AC边上的友好圆的半径为 ．

（2）如图2，已知等腰△ABC，AB=AC=10，BC=12，画草图并求出它所有的友好圆的半径．

Answer 1

【答案】⑴6 ;⑵

【解析】

（1）先依据勾股定理求得AC的长，然后依据切线的性质可知AC为圆的直径，故此可求得△BAC的友好圆的半径等于AC的一半；

（2）当O在BC上时，连接OD，过点A作AE⊥BC．由等腰三角形的性质和勾股定理求得AE=8，依据切线的性质可证明OD⊥AB，接下来证明△ODB∽△AEB，由相似三角形的性质可求得圆O的半径；当O在AB上且圆O与BC相切时，连接OD、过点A作AE⊥BC，垂足为E．先证明△BOD∽△BAE，由相似三角形的性质可求得圆O的半径，当O在AB上且圆O与AC相切时，连接OD、过点B作BF⊥AC，过点A作AE⊥BC，垂足为E．先依据面积法求得BF的长，然后再证明△AOD∽△ABF，由相似三角形的性质可求得圆O的半径；

（1）∵∠C=90°，AB=13，BC=5，

∴AC=．

∵BC是圆的切线，∠BCA=90°，

∴AC为圆的直径．

∴AC边上的半随圆的半径为6．

（2）当O在BC上时，如图（1）所示：连接OD，过点A作AE⊥BC．

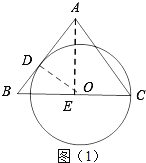
∵AB=AC，AE⊥BC，

∴BE=EC=6．

在△AEB中，由勾股定理可知AE==8．

∵AB与⊙O相切，

∴OD⊥AB．

∴∠BDO=∠BEA=90°．

又∵∠OBD=∠EBA，

∴△ODB∽△AEB．

∴．

设⊙O的半径为r．在OB=12-r．

∴．

∴r=．

∴△ABC的BC边上的友好圆的半径为．

当O在AB上时，如图（2），连接OD、过点A作AE⊥BC，垂足为E．

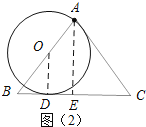
∵BC与⊙O相切，

∴OD⊥BC．

又∵AE⊥BC，

∴OD∥AE．

∴△BOD∽△BAE．

∴．

设⊙O的半径为r，则OB=10-r．

∴．

∴r=．

如图（3）所示：连接OD、过点B作BF⊥AC，过点A作AE⊥BC，垂足为E．

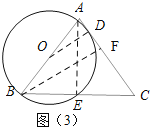
∵S△ABC=BCAE=ACBF，

∴×12×8=×10×BF．

∴BF=9.6．

∵AC与⊙O相切，

∴DO⊥AC．

∴DO∥BF．

∴△AOD∽△ABF．

∴

即．

∴r=．

综上所述，△ABC的友好圆的半径分为．