题目内容
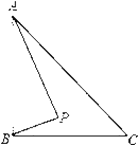
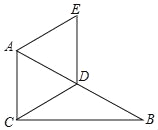
【题目】如图，已知Rt△ABC中，∠ACB＝90°，∠B＝30°，D是AB的中点，AE∥CD，AC∥ED，
求证：四边形ACDE是菱形．
【答案】证明见解析.
【解析】
由AE∥CD，AC∥ED可证四边形ACDE是平行四边形，
由直角三角形斜边上的中线等于斜边的一半可得CD＝
AB＝AD，
由∠ACB＝90°，∠B＝30°，可得∠CAB＝60°，即可证△ACD为等边三角形，由此可得AC＝CD，即可证平行四边形ACDE是菱形．
∵AE∥CD，AC∥ED，
∴四边形ACDE是平行四边形，
∵∠ACB＝90°，D为AB的中点，
∴CD＝AB＝AD，
∵∠ACB＝90°，∠B＝30°，
∴∠CAB＝60°，
∴△ACD为等边三角形，
∴AC＝CD，
∴平行四边形ACDE是菱形．
练习册系列答案
相关题目
【题目】九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”， “5”，“6”的四张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为x，按表格要求确定奖项．
奖项 | 一等奖 | 二等奖 | 三等奖 |
|x| | |x|=4 | |x|=3 | 1 |
（1）用列表或画树状图的方法求出甲同学获得一等奖的概率；
（2）求出每次抽奖获奖的概率？
