题目内容
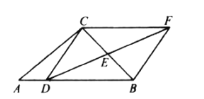
【题目】如图,在![]() 中,D是AB上任意一点,E是BC的中点,过C作
中,D是AB上任意一点,E是BC的中点,过C作![]() ,交DE的延长线于F,连BF,CD,若
,交DE的延长线于F,连BF,CD,若![]() ,
,![]() ,
,![]() ,则
,则![]() _________.
_________.
【答案】4
【解析】
证明CF∥DB,CF=DB,可得四边形CDBF是平行四边形,作EM⊥DB于点M,解直角三角形即可.
解:∵CF∥AB,
∴∠ECF=∠EBD.
∵E是BC中点,
∴CE=BE.
∵∠CEF=∠BED,
∴△CEF≌△BED(ASA).
∴CF=BD.
∴四边形CDBF是平行四边形.
作EM⊥DB于点M,

∵四边形CDBF是平行四边形,![]() ,
,
∴BE=![]() ,DF=2DE,
,DF=2DE,
在Rt△EMB中,EM2+BM2=BE2且EM=BM
∴EM=1,
在Rt△EMD中,
∵∠EDM=30°,
∴DE=2EM=2,
∴DF=2DE=4.
故答案为:4.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目