题目内容
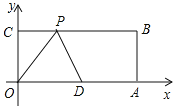
【题目】我市某企业接到一批产品的生产任务,按要求必须在14天内完成.已知每件产品的出厂价为60元.工人甲第x天生产的产品数量为y件,y与x满足如下关系:
![]()
(1)工人甲第几天生产的产品数量为70件?
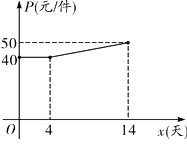
(2)设第x天生产的产品成本为P元/件,P与![]() 的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
的函数图象如图.工人甲第x天创造的利润为W元,求W与x的函数关系式,并求出第几天时利润最大,最大利润是多少?
【答案】(1)工人甲第12天生产的产品数量为70件;(2)第11天时,利润最大,最大利润是845元.
【解析】(1)根据y=70求得x即可;(2)先根据函数图象求得P关于x的函数解析式,再结合x的范围分类讨论,根据“总利润=单件利润×销售量”列出函数解析式,由二次函数的性质求得最值即可.
本题解析:
解:(1)若7.5x=70,得x=![]() >4,不符合题意;
>4,不符合题意;
则5x+10=70,
解得x=12.
答:工人甲第12天生产的产品数量为70件.
(2)由函数图象知,当0≤x≤4时,P=40,
当4<x≤14时,设P=kx+b,
将(4,40)、(14,50)代入,得![]() 解得
解得![]()
∴P=x+36.
①当0≤x≤4时,W=(60-40)·7.5x=150x,
∵W随x的增大而增大,
∴当x=4时,W最大=600;
②当4<x≤14时,W=(60-x-36)(5x+10)=-5x2+110x+240=-5(x-11)2+845,
∴当x=11时,W最大=845.
∵845>600,
∴当x=11时,W取得最大值845元.
答:第11天时,利润最大,最大利润是845元.

【题目】蚌埠“一带一路”国际龙舟邀请赛期间,小青所在学校组织了一次“龙舟”故事知多少比赛,小青从全体学生中随机抽取部分同学的分数(得分取正整数,满分为100分)进行统计.以下是根据抽取同学的分数制作的不完整的频率分布表和频率分布直方图,请根据图表,回答下列问题: :
组别 | 分组 | 频数 | 频率 |
1 |
| 9 | 0.18 |
2 |
|
|
|
3 |
| 21 | 0.42 |
4 |
|
| 0.06 |
5 |
| 2 |
|

(1)根据上表填空: ![]() __,
__,![]() =. ,
=. ,![]() = .
= .
(2)若小青的测试成绩是抽取的同学成绩的中位数,那么小青的测试成绩在什么范围内?
(3)若规定:得分在![]() 的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?
的为“优秀”,若小青所在学校共有600名学生,从本次比赛选取得分为“优秀”的学生参加决赛,请问共有多少名学生被选拔参加决赛?