题目内容
【题目】某汽车厂决定把一块长100m、宽60m的矩形空地建成停车场．设计方案如图所示，阴影区域为绿化区（四块绿化区为全等的矩形），空白区域为停车位，且四周的4个出口宽度相同，其宽度不小于28m，不大于52m．设绿化区较长边为xm，停车场的面积为ym2
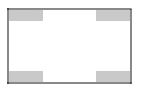
（1）直接写出：
①用x的式子表示出口的宽度为_____．
②y与x的函数关系式及x的取值范围．
（2）求停车场的面积y的最大值．
（3）预计停车场造价为100元/m2，绿化区造价为50元/m2．如果汽车厂投资不得超过540000元建造，当x为整数时，共有几种建造方案？
【答案】（1）①（100﹣2x）m；②y＝﹣4x2+80x+6000（24≤x≤36）；（2）5616m2；（3）共有3种建造方案．
【解析】
（1）①根据图形可得结论；②根据题意可得y与x的关系式；
（2）根据二次函数的增减性可得结论；
（3）根据列方程即可得到结论．
解：（1）①出口的宽度为：100﹣2x，
②根据题意得，y＝100×60﹣4x（x﹣20），
即y与x的函数关系式及x的取值范围为：y＝﹣4x2+80x+6000（24≤x≤36）；
故答案为：（100﹣2x）m；
（2）y＝﹣4x2+80x+6000＝﹣4（x﹣10）2+6400，
∵a＝﹣4＜0，抛物线的开口向下，对称轴为x＝10，当24≤x≤36时，y随x的增大而减小，
∴当x＝24时，y最大＝5616，
答：停车场的面积y的最大面积为5616m2；
（3）设费用为w，
由题意得，w＝100（﹣4x2+80x+6400）+50×4x（x﹣20）＝﹣200（x﹣10）2+660000，
∴当w＝540000时，解得：x1＝﹣10
+10，x2＝10+10，
∵a＝﹣100＜0，
∴x1＝﹣10+10，x2＝10+10，w＝540000，
∵24≤x≤36，
∴10+10≤x≤36，且x为整数，
∴共有3种建造方案．
