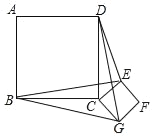
题目内容
【题目】已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;

(1)如图1, BD⊥CD,∠DCA=30°,则∠BAD=
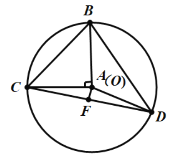
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=![]() ,求△BCD的面积.
,求△BCD的面积.
【答案】(1)15°;(2)见详解;(3)![]() .
.
【解析】
(1)先求出∠BCD的大小,然后通过两条边对应成比例且夹角相等得到△CEB∽△AED,得到∠BAD=∠BCD,即可求得∠BAD的大小;
(2)作△BCD的外接圆,通过圆周角定理得到点A即为该圆的圆心,即可知道AC=AD,从而证得AF⊥CD;
(3)过点D作DE⊥BC于点E,通过∠BDA=3∠CBD得到BD为∠ABC的平分线,从而得到DE=AD,然后利用勾股定理求得DE的值,再求得BC的长度,即可得到三角形面积.
解:(1)∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠DCA=30°,
∴∠BCD=45°-30°=15°,
又∵BD⊥CD,
∴∠CBD=90°-15°=75°,
∴∠ABD=75°-45°=30°,
在Rt△ACE和Rt△BDE中,∠ACE=30°,∠ABD=30°,
∴![]() ,
, ![]() ,
,
在△CEB和△AED中,
∠CEB=∠AED,![]() ,
,
∴△CEB∽△AED,
∴∠BAD=∠BCD=15°.
(2)如图,作三角形BCD的外接圆,则∠BCD为圆周角,
∵∠BDC=45°,
∴![]() 所对的圆心角为90°,
所对的圆心角为90°,
∵∠BAC=90°,
∴点A即为△BCD的外接圆的圆心,
∴AC=AD,
∵点F是CD中点,
∴AF⊥CD.
(3)如图,过点D作DE⊥BC于点E,
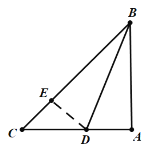
∵AB=AC,∠BAC=90°,
∴∠ABC=∠ACB=45°,
∵∠BDA=3∠CBD,∠BDA=∠C+∠CBD,
∴∠C=2∠CBD,
∵∠ABC=∠ACB,∠ABC=∠ABD+∠CBD,
∴∠ABD=∠CBD,
又∵∠BAC=90°,DE⊥BC,
∴DE=AD,
设DE=AD=a,
易得△CED为等腰直角三角形,
∴CD=![]() ,
,
∴AB=AC=![]() ,
,
∵BD=![]() ,
,
∴在Rt△ABD中,![]() ,
,
解得 ![]() ,
,
∴AB=AC=![]() ,
,
∴BC=![]() ,
,
∴ .
.