题目内容
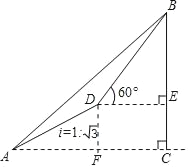
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).

【答案】BC= 100+100![]() (米).
(米).
【解析】
作DF⊥AC于F,根据i=1:![]() ,AD=200米,可知tan∠DAF=
,AD=200米,可知tan∠DAF=![]() ,可知∠DAF=30°,进而求出DF的长度,根据所给角的度数可知△ABD是等腰三角形,AD=BD,解直角三角形BDE可求出BE,根据BC=BE+CE求出BC即可.
,可知∠DAF=30°,进而求出DF的长度,根据所给角的度数可知△ABD是等腰三角形,AD=BD,解直角三角形BDE可求出BE,根据BC=BE+CE求出BC即可.
作DF⊥AC于F.
∵DF:AF=1:![]() ,AD=200米,
,AD=200米,
∴tan∠DAF=![]() ,
,
∴∠DAF=30°,
∴DF=![]() AD=
AD=![]() ×200=100(米),
×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=![]() ,
,
∴BE=BDsin∠BDE=200×![]() =100
=100![]() (米),
(米),
∴BC=BE+EC=100+100![]() (米).
(米).

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目







